Order Theory

Table of Contents

• Ordered Relations
  • Partial Order Relation
  • Total Order Relation
• Partial and Total Orderings
  • Partially Ordered Set (POSET)
  • Comparability
  • Totally Ordered Set (TOSET)
• Supremum and Infimum
  • Supremum (Least Upper Bound)
  • Infimum (Greatest Lower Bound)
• Minimal and Maximal elements
  • Minimal element
  • Maximal element
• Minimum and Maximum elements
  • Minimum element
  • Maximum element
• Lattices
  • Join Semi Lattice
  • Meet Semi Lattice
  • Lattice
• Hasse Diagram
  • Why is it called a lattice?
• Types of lattice
  • Bounded lattice
    • Complement of an element in a lattice
  • Sublattice
  • Complemented Lattice
  • Distributive Lattice
• Boolean Algebra
• Questions

Ordered Relations

Partial Order Relation

A relation $R$ on $A$ is a partial order relation if and only if -

1. $R$ is reflexive
2. $R$ is anti-symmetric
3. $R$ is transitive

Total Order Relation

Let $R$ be a partial order relation on $A$. $R$ is called a total order relation if every pair of elements of $A$ are comparable w.r.t $R$.

Example - Let $A=\{1,2,3,4\}$ and $(A,÷)$ be a POSET. Here as 2 doesn’t divide 3 and 3 doesn’t divide 2, 2 and 3 are not comparable. Thus $A$ is not a total order relation.

See Question 4 for a property.

Partial and Total Orderings

Partially Ordered Set (POSET)

A pair $(A,R)$ is a partially ordered set (POSET), if and only if $R$ is a partial order relation defined on a set $A$.

Example - $(A,\le )$ is a POSET for any set $A$ as $\le$ is a partial order relation.

Comparability

Let $R$ be a relation on some set $A$. For any two elements $a,b\in A$, we say $a$ and $b$ are comparable if and only if $a^{R}b$ or $b^{R}a$.

Totally Ordered Set (TOSET)

A pair $(A,R)$ is a totally ordered set (TOSET), if and only if $(A,R)$ is a POSET and every pair of elements of $A$ is comparable w.r.t relation $R$.

Also called as Linearly Ordered Sets because of their Hasse Diagrams.

Supremum and Infimum

Check Question 1 and Question 2 for example.

Supremum (Least Upper Bound)

For POSET $(A,\le )$, for any two elements $a,b\in A$ we can say $c$ is the supremum/Least Upper Bound of $a$ and $b$, if -

$$\begin{array}{rl}& \exists c\in A\text{s.t.}a\le c,b\le c\\ \text{and}& \nexists d\in A\text{s.t.}a\le d,b\le d,d\le c\end{array}$$

For any general relation $R$ -

$$\begin{array}{rl}& \exists c\in A\text{s.t.}{a}^{R}c,b^{R}c\\ \text{and}& \nexists d\in A\text{s.t.}{a}^{R}d,b^{R}d,d^{R}c\end{array}$$

This is denoted as $lub(a,b)=c$ or $a\vee b=c$.

Infimum (Greatest Lower Bound)

For POSET $(A,\le )$, for any two elements $a,b\in A$ we can say $c$ is the infimum/Greatest Lower Bound of $a$ and $b$, if -

$$\begin{array}{rl}& \exists c\in A\text{s.t.}c\le a,c\le b\\ \text{and}& \nexists d\in A\text{s.t.}d\le a,d\le a,c\le d\end{array}$$

For any general relation $R$ -

$$\begin{array}{rl}& \exists c\in A\text{s.t.}{c}^{R}a,c^{R}b\\ \text{and}& \nexists d\in A\text{s.t.}{d}^{R}a,d^{R}a,c^{R}d\end{array}$$

This is denoted as $gub(a,b)=c$ or $a\wedge b=c$.

Minimal and Maximal elements

Can be multiple.

Minimal element

For POSET $(A,\le )$, we can say $x$ is a minimal element of $A$ if $x\in A$ and $\nexists y$ such that $y<x$ other than $y=x$.

For any general POSET $(A,R)$, $x$ is a minimal element if $\nexists y$ such that $y^{R}x$ and $y\ne x$.

Maximal element

For POSET $(A,\le )$, we can say $x$ is a maximal element of $A$ if $x\in A$ and $\nexists y$ such that $y>x$ other than $y=x$.

For any general POSET $(A,R)$, $x$ is a maximal element if $\nexists y$ such that $x^{R}y$ and $y\ne x$.

Minimum and Maximum elements

On the lower side or greater side than all other elements.

Minimum element

For POSET $(A,\le )$, we can say $x$ is the minimum element of $A$ if $x\in A$ and $\forall y\in A$ such that $x\le y$.

For any general POSET $(A,R)$, $\exists x$ such that $x^{R}y,\forall y\in A$, then we say $x$ is the minimum element.

Important Properties -

1. If there are two or more minimal elements in a POSET, then there will not exist any minimum element.
2. If there exist a unique minimal element in a POSET, then that element will also be the minimum element of the POSET.

Maximum element

For POSET $(A,\le )$, we can say $x$ is the maximum element of $A$ if $x\in A$ and $\forall y\in A$ such that $x\ge y$.

For any general POSET $(A,R)$, $\exists x$ such that $y^{R}x,\forall y\in A$, then we say $x$ is the maximum element.

Important Properties -

1. If there are two or more maximal elements in a POSET, then there will not exist any maximum element.
2. If there exist a unique maximal element in a POSET, then that element will also be the maximum element of the POSET.

Lattices

Join Semi Lattice

A POSET in which least upper bound exists for every pair of elements is called a join semi lattice.

Meet Semi Lattice

A POSET in which greatest lower bound exists for every pair of elements is called a meet semi lattice.

Lattice

A lattice is an algebraic structure $[L,\vee ,\wedge ]$ such that a least upper bound and greatest lower bound exit for every pair of elements.

$(OR)$

A POSET which is a join semi lattice as well as a meet semi lattice is called a lattice.

A lattice holds the following properties -

1. Commutative Property -

$$\begin{array}{rl}a\vee b& =b\vee a\\ a\wedge b& =b\wedge a\end{array}\forall a,b\in L$$

2. Associative Property -

$$\begin{array}{rl}(a\vee b)\vee c& =a\vee (b\vee c)\\ (a\wedge b)\wedge c& =a\wedge (b\wedge c)\end{array}\forall a,b\in L$$

3. Idempotent Law -

$$\begin{array}{rl}a\vee a& =a\\ a\wedge a& =a\end{array}\forall a,b\in L$$

4. Absorption Law -

$$\begin{array}{rl}a\vee (a\wedge b)& =a\\ a\wedge (a\vee b)& =a\end{array}\forall a,b\in L$$

5. Distributive property need not hold true for every lattice. Any lattice for which the distributive property holds true for every triple of elements is called a distributive lattice.

$$\begin{array}{rl}a\vee (b\wedge c)& =(a\vee b)\wedge (a\vee c)\\ a\wedge (b\vee c)& =(a\wedge b)\vee (a\wedge c)\end{array}\forall a,b\in L$$

Hasse Diagram

A Hasse Diagram is a visual representation of a finite partially ordered set (POSET). In a Hasse diagram of a POSET -

1. Create a vertex corresponding to every element in the underlying set of the POSET.
2. Add an edge between any two vertices only if $a^{R}b$ such that $\nexists x$ such that $a^x,x^b$ (No edges for transitive relations, transitivity is implied).
3. Don’t add edges for any self loop (reflexivity is implied).
4. Edges can be directed or undirected. If left undirected, it implies an upward orientation. Meaning if $a^{R}b$ then $b$ is above $a$.

Cases -

1. A Hasse Diagram for a TOSET would always be a linear chain. Thus they are called Linearly Ordered Sets.
2. The least upper bound (supremum) of two elements $a$ and $b$, if it exists, is the lowest vertex that lies above both $a$ and $b$.
3. The greatest lower bound (infimum) of two elements $a$ and $b$, if it exists, is the highest vertex that lies below both $a$ and $b$.
4. The top most element in a Hasse Diagram is the maximum element. However, if more than one elements are the top most elements then the POSET has no maximum element, only maximal elements.
5. The bottom most element in a Hasse Diagram is the minimum element. However, if more than one elements are the bottom most elements then the POSET has no minimum element, only minimal elements.

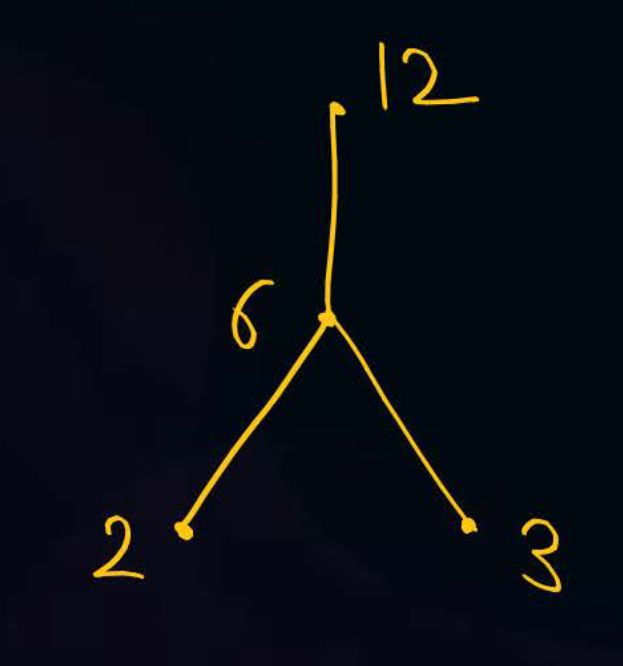
In the above Hasse Diagram -

1. 6 is the supremum of 2 and 3.
2. 6 is the infimum of 6 and 12.
3. 12 is the maximum element.
4. 2 and 3 are the minimal elements.

Why is it called a lattice?

POSETs with both an infimum and a supremum are called a lattice because, in a Hasse diagram, the elements form a criss-cross (grid-like) structure where every pair of elements has a well-defined meet and join, resembling the bars of a physical lattice.

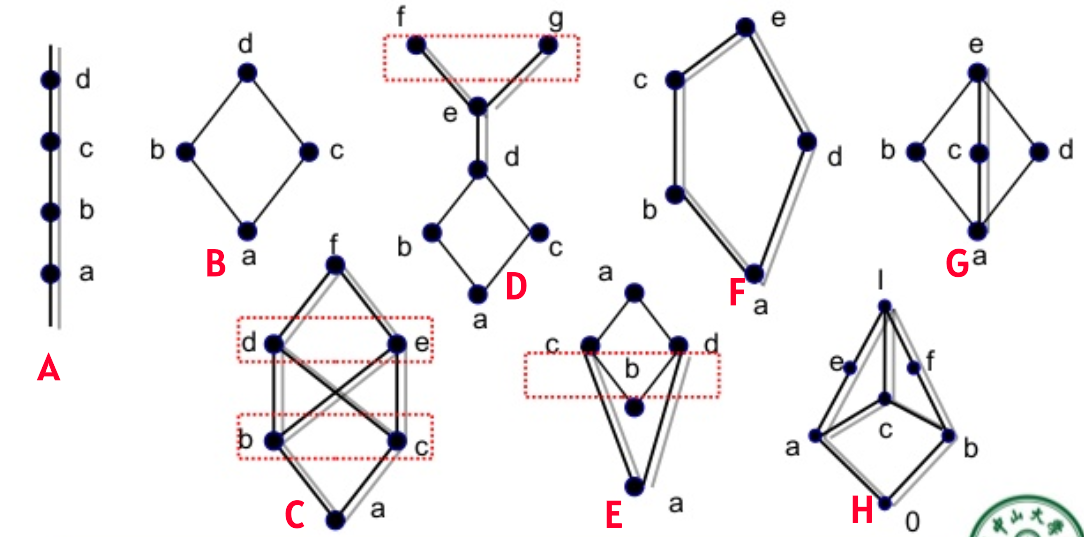
In the above diagram -

1. $A$ is a TOSET due to the linear Hasse Diagram.
2. $D$ is a meet semi lattice. A meet semi lattice is called that way because for every pair of elements, the downward paths always meet at a unique greatest lower bound (meet), whereas the upward paths may fail to meet at a least upper bound (join).
3. $B,C,E,F,G,H$ are all both meet semi lattice and join semi lattice; hence, each of them is a lattice.

Types of lattice

Bounded lattice

Let $[L,\vee ,\wedge ]$ be a lattice -

• If there exists an element $I\in L$ such that $a\vee I=I,\forall a\in L$, then $I$ is called the universal upper bound of the lattice $L$.
• If there exists an element $O\in L$ such that $a\wedge O=O,\forall a\in L$, then $O$ is called the universal lower bound of the lattice $L$.

If both $I$ and $O$ exist for a lattice $L$, then $L$ is called a bounded lattice.

Example - In lattice w.r.t POSET $(D_{12},÷)$ where $D_{12}$ means the set of all divisors of 12 -

• 12 is the universal upper bound.
• 1 is the universal lower bound.
• Thus $L$ is a bounded lattice.

Properties -

• A lattice need not always be bounded as for some lattices the upper bound or lower bound might not exist. Example - $(\mathbb{R},\le )$ is a lattice as each pair of elements has an infimum and a supremum, but the maximum and minimum don’t exist for this lattice.
• If a lattice is unbounded, then the underlying set will be an infinite set. But the converse is not true. Example - $\{x:x\in \mathbb{R}\text{and}0\le x\le 1\}$ is an infinite set but also bounded.

Complement of an element in a lattice

Let $[L,\vee ,\wedge ]$ be a bounded lattice with $I$ as the universal upper bound and $O$ as the universal lower bound -

• For an element $a\in L,\exists b\in L$ such that $a\vee b=I$ and $a\wedge b=O$, then $a$ and $b$ are complement of each other.
• A complement of an element need not exist and if it exists then it need not be unique.

Notes -

• $I\vee O=I$ and $I\wedge O=O$, thus $I$ and $O$ are complement of each other. No other complement exists for them.
• In a bounded TOSET, only $I$ and $O$ are complements of each other. Other than these, no other elements have a complement. An easy way to visualize why this happens is because the Hasse Diagram for a TOSET is a linear chain.

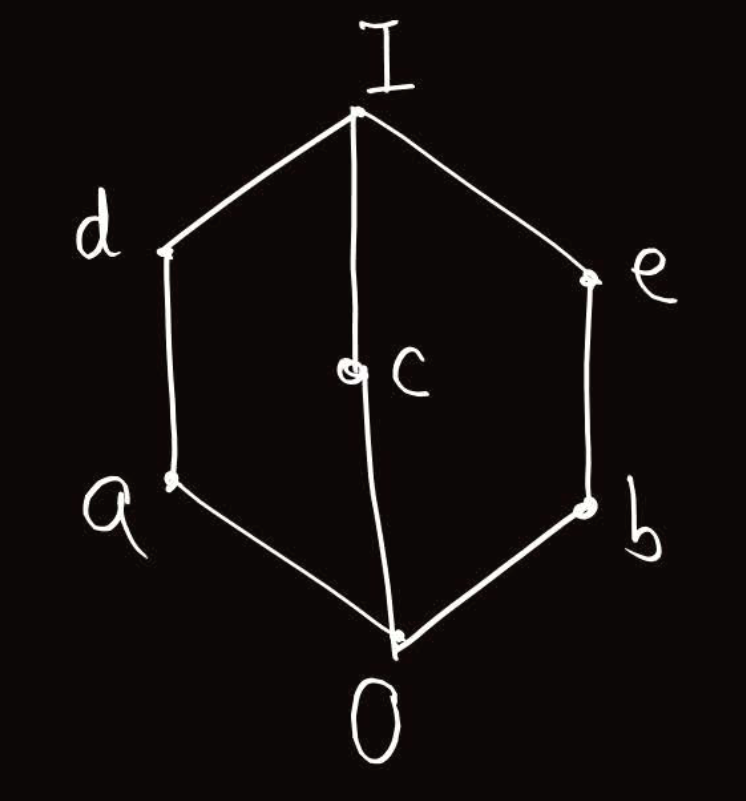
In the above bounded lattice -

• $\bar{a}=b,c,e$
• $\bar{b}=a,c,d$
• $\bar{c}=a,b,d,e$
• $\bar{d}=b,c,e$
• $\bar{e}=a,c,d$

Sublattice

Let $[L,\vee ,\wedge ]$ be a lattice. A subset $M$ of set $L$ such that the $[M,\vee ,\wedge ]$ is a sublattice of lattice $L$ if and only if -

• The supremum and infimum for every pair of elements of lattice $M$ is the same as the supremum and infimum for these same elements in lattice $L$.

Complemented Lattice

A lattice in which a complement exists for every element of the lattice. Complement need not be unique, just needs to exist.

Distributive Lattice

A lattice is a distributive lattice if and only if the distributive property of lattices applies to it.

In a distributive lattice, an element can have 0 or 1 complement.

• So to check whether a lattice is distributive or not, instead of applying the distributive property for all triples of elements, it is more efficient to calculate the number of complements for each element and check whether this count is either 0 or 1.
• Any lattice with 4 or less elements is always distributive.

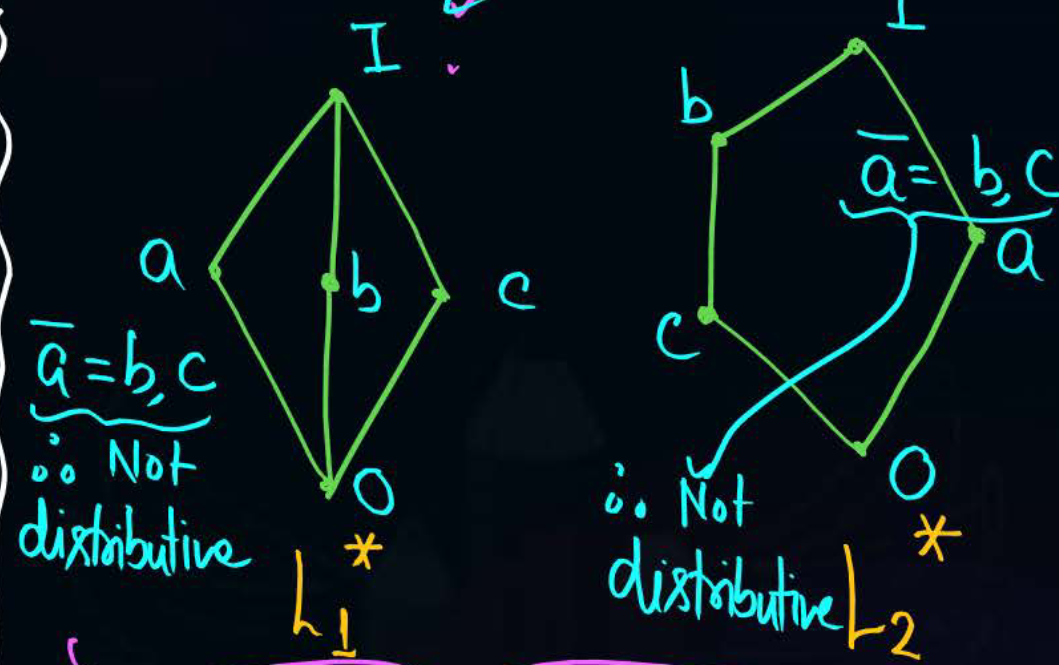
• If a lattice $L$ has any sublattice which is isomorphic (similar) to either $L_1^{\ast }$ or $L_2^{\ast }$ then we can say that $L$ is not distributive.
• If a lattice $L$ is distributive, then all its sublattices will be distributive.

Boolean Lattice/Boolean Algebra

A lattice which is complemented as well as distributive is called a Boolean lattice or Boolean Algebra. Meaning that in a Boolean lattice every element has exactly one complement.

Special Examples -

1. $(P(A),\subseteq )$ is a boolean lattice as each element has exactly one complement.
2. A square free integer is a positive integer such that none of its divisors (except 1) is a square. If $n$ is square free then $D_n$ is a boolean lattice where for some $x\in D_n$, $\bar{x}=\frac{n}{x}$.

---

Questions

Q1) If A is a set of all +ve integers, find the supremum and infimum of POSETS -

$$(A,\le ),(A,÷),\text{and}(A,\subseteq )$$

$\underline{{\text{Sol}}^n}-$

1. $(A,\le )$, for $a,b\in A$ -
   1. $lub(a,b)=max(a,b)$
   2. $glb(a,b)=min(a,b)$
2. $(A,÷)$, for $a,b\in A$ -
   1. $lub(a,b)=LCM(a,b)$ ($lub(a,b)$ in context of $÷$ means that the supremum is divisible by both $a$ and $b$)
   2. $glb(a,b)=GCD(a,b)$ ($glb(a,b)$ in context of $÷$ means that the infimum divides both $a$ and $b$)
3. $(A,\subseteq )$, for $a,b\in A$ -
   1. $lub(a,b)=a\cup b$ ($lub(a,b)$ in context of $\subseteq$ means that $a$ and $b$ both are subsets of the supremum)
   2. $glb(a,b)=a\cap b$ ($glb(a,b)$ in context of $\subseteq$ means that the infimum is a subset of $a$ and $b$ both)

---

Q2) For POSET (A, subset operation) where A = {{1}, {2}, {1,2,3}, {1,2,4}} what is lub({1}, {2})?

$\underline{{\text{Sol}}^n}-$ Here $\{1\}$ and $\{2\}$ both are subsets of $\{1,2,3\}$ and $\{1,2,4\}$. Because $\{1,2,3\}$ and $\{1,2,4\}$ aren’t comparable in the context of relation $\subseteq$ and because both aren’t equal, we can’t decide on a supremum.

Thus $lub(1,2)$ $\boxed{\text{doesn’t exist}}$ for the POSET.

---

Q3) For POSET (A, division operation) where A = {2,3,4,5} what are the maximal and minimal element(s)?

$\underline{{\text{Sol}}^n}-$

• Minimal Elements - $\boxed{2,3,\text{and}5}$ because there don’t exist any other elements less than these who divides them.
• Maximal Elements - $\boxed{3,4,\text{and}5}$ because there don’t exist any other elements greater than these which are divisible by them.

---

Q4) How many Total Order Relations are possible on a set with n element?

$\underline{{\text{Sol}}^n}-$ A Hasse diagram of a TOSET is a linear chain with each element as a vertex of this chain. The elements can be move around in a total of $n!$ ways, with each permutation being a new Hasse Diagram corresponding a new TOSET. Thus total number of relations is $\boxed{n!}$.