Asymptotic Notation

Table of Contents

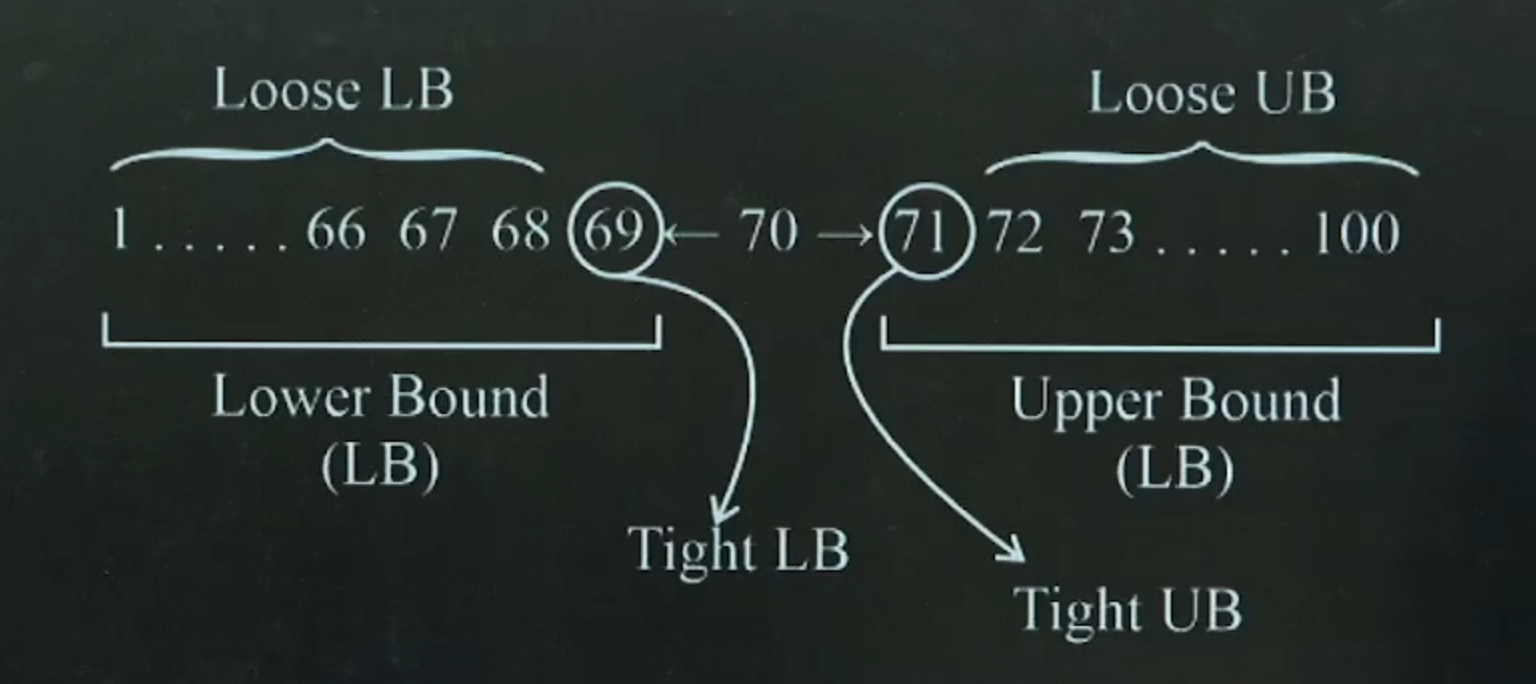
• Types of Bound
• Types of Notations
• Big Notations
  • 1. Big Oh
  • 2. Big Omega
  • 3. Big Theta
• Small Notations
  • 1. Small Oh
  • 2. Small Omega
• Properties of Asymptotic Notations
  • General Properties of Big Oh Notation
  • Adding Functions
  • Multiplying Functions
  • Trichotomy Property
  • Discrete Properties of Asymptotic Notations

Types of Bound

1. Upper Bound -
   1. Tight Upper Bound
   2. Loose Upper Bound
2. Lower Bound -
   1. Tight Lower Bound
   2. Loose Lower Bound

Types of Notations

1. Big Notation - Bounds that may or may not be tight.
   1. Big Oh $\to O$
   2. Big Omega $\to \Omega$
2. Small Notation - Bound that are always loose, never tight
   1. Small Oh $\to o$
   2. Small Omega $\to \omega$

Big Notations

The big notations always provide lower/upper bound that may or may not be tight.

1. Big Oh $(O)$

$f(n)=O(g(n))$ if there exists some constant $c>0$ and $n_0>0$ such that - $f(n)\le c\ast g(n);\forall n\ge n_0$ In simpler words this means – For large values of $n$, the growth of function $f(n)$ is bounded above by a constant multiple of $g(n$).

---

Q1) Show that -

$f(n)=n^2+n+1=O(n^2)$ Sol${}^n$ - We know that -

1. $n^2\ge n^2$
2. $n^2\ge n$
3. $n^2\ge 1;\forall n\ge 1$

Thus $n^2+n+1\le 3n^2$ where $c=3$ and $n_0=1$. Thus $f(n)=O(n^2)$.

$Q.E.D.$

---

2. Big Omega $(\Omega )$

$f(n)=\Omega (g(n))$ if there exists some constant $c>0$ and $n_0>0$ such that - $f(n)\ge c\ast g(n);\forall n\ge n_0$ In simpler words this means – For large values of $n$, the growth of function $f(n)$ is bounded below by a constant multiple of $g(n$).

3. Big Theta $(\Theta )$

$f(n)=\Theta (g(n))$ if there exists some constant $c_1>0,c_2>0$ and $n_0>0$ such that - $c_1\ast g(n)\le f(n)\le c_2\ast g(n);\forall n\ge n_0$ In simpler words – When for large values of $n$ the growth of $f(n)$ is bounded above and below by constant multiples of the same function $g(n)$, we say $g(n)$ is the Tight-Bound of $f(n)$.

$f(n)=O(g(n))$ and $f(n)=\Omega (g(n))$.

---

Q2) Find the tight bound of the below function -

$f(n)={\sum }_{a=1}^n{\left(\frac{1}{5}\right)}^a$

Sol${}^n$ - Using the Sum of GP $f(n)=\frac{1}{4}\left(1-\frac{1}{5^n}\right)$ As ${\lim }_{n\to \infty }f(n)=\frac{1}{4}$, $f(n)=\Theta (1)$

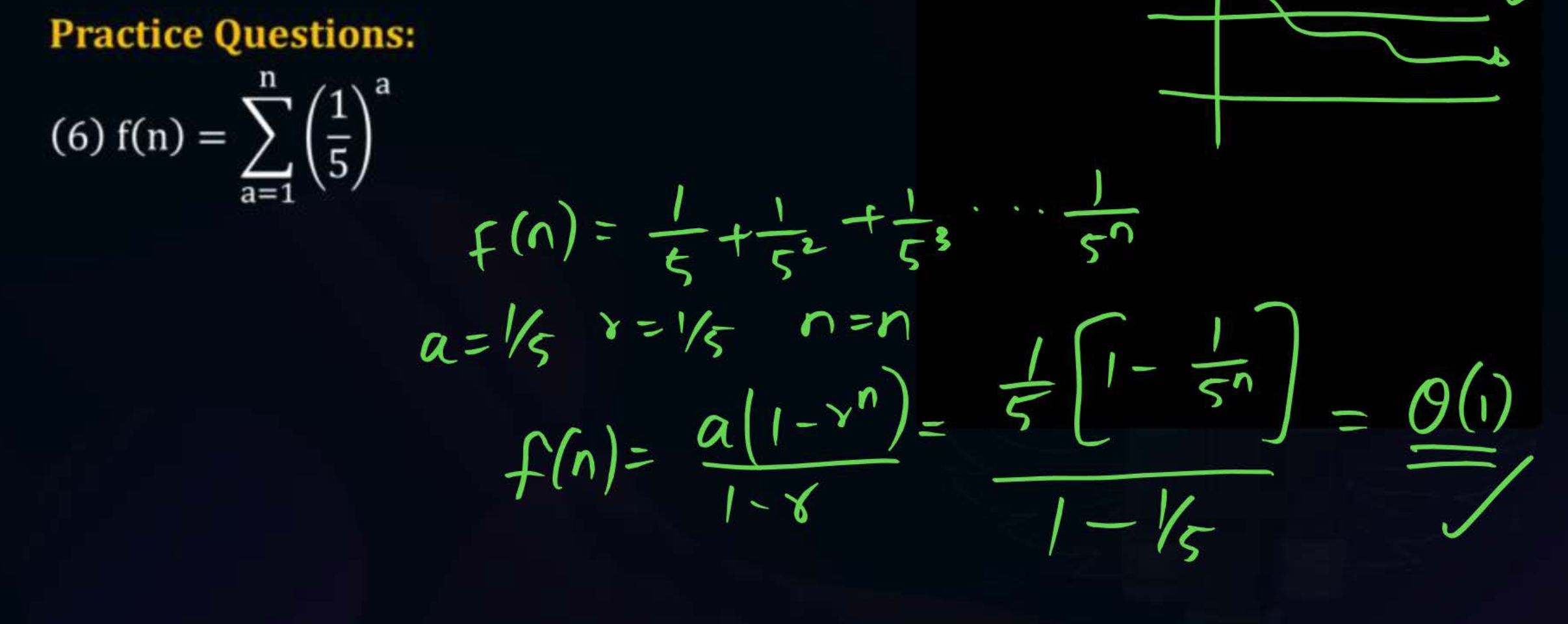
Another reasoning can be that $\frac{1}{5}$ being a constant dominated the decreasing function $1-\frac{1}{5^n}$.

---

Q3) Find the tight bound of the below function -

Sol${}^n$ -

• Here, $f(n)=n!$. For each $i$ in the product, we can say $i\le n$. Thus $n!=O(n^n)$.
• At the same time $n\ast (n-1)\ast (n-2)\ast \cdots \ast 1\ngeqq c\ast n^n$ for any value of $c$. Thus $f(n)\ne \Omega (n)$ and thus $f(n)\ne \Theta (n)$.

---

Q4) Find the tight bound of the below function -

$f(n)={\sum }_{a=1}^{n}logi$ Sol${}^n$ -

$$\begin{array}{rl}\sum _{a=1}^{n}logi& =log(1)+log(2)+\cdots +log(n)\\ & =log(1\ast 2\ast \cdots \ast n)\\ & =log(n!)\end{array}$$ $$\begin{array}{rl}log(n)& \le log(n)\\ log(n)+log(n-1)+\cdots +log(1)& \le log(n)+log(n)+\cdots +log(n)\\ log(n!)& \le n\cdot log(n)\\ log(n!)& =O(n\cdot log(n))\end{array}$$

---

Small Notations

The big notations always provide lower/upper bound that are loose, never tight.

1. Small Oh $(o)$

$f(n)=o(g(n))$ if there exists all constant $c>0$ and some $n_0\ge 0$ such that - $f(n)<c\ast g(n);\forall n\ge n_0$ In simple words – $f(n)$ grows strictly slower than $g(n)$, and no constant multiple of $g(n)$ is a tight bound for $f(n)$.

Key Difference from $O$ -

1. The inequality constraint must satisfied for all positive constants, not some.
2. The inequality constraint is a strict inequality.

2. Small Omega $(\omega )$

$f(n)=\omega (g(n))$ if for all constant $c>0$ and some $n_0\ge 0$ such that - $f(n)>c\ast g(n);\forall n\ge n_0$ In simple words – $f(n)$ grows strictly faster than $g(n)$, and no constant multiple of $g(n)$ is a tight bound for $f(n)$.

Properties of Asymptotic Notations

General Properties of Big Oh Notation

1. If $d(n)=O(f(n))$ $\to$ $a\cdot d(n)=O(f(n))$
2. If $d(n)=O(f(n))$ and $e(n)=O(g(n))$ $\to$ $d(n)+e(n)=O(f(n)+g(n))$
3. If $d(n)=O(f(n))$ and $e(n)=O(g(n))$ $\to$ $d(n)\cdot e(n)=O(f(n)\cdot g(n))$
4. If $d(n)=O(f(n))$ and $f(n)=O(g(n))$ $\to$ $d(n)=O(g(n))$
5. $n^x=O(a^n)$ for any fixed $x>0$ and $a>1$
6. $log(n^x)=O(log(n))$ for any fixed $x>0$
7. $lo{g}^x(n)=O(n^y)$ for any fixed constants $x>0$ and $y>0$

Adding Functions

1. $O(f(n))+O(g(n))\to O(max(f(n),g(n))$
2. $\Omega (f(n))+\Omega (g(n))\to \Omega (max(f(n),g(n))$
3. $\Theta (f(n))+\Theta (g(n))\to \Theta (max(f(n),g(n))$

Multiplying Functions

1. $O(f(n))\ast O(g(n))\to O(f(n)\ast g(n))$
2. $\Omega (f(n))\ast \Omega (g(n))\to \Omega (f(n)\ast g(n))$
3. $\Theta (f(n))\ast \Theta (g(n))\to \Theta (f(n)\ast g(n))$

Trichotomy Property

The Trichotomy Property for real numbers says that for any two real numbers $x$ and $y$ only one of the three cases is true -

1. $x>y$
2. $x=y$
3. $x<y$

The Asymptotic Notations do not define a total order on functions and therefore do not satisfy the Trichotomy Property. For any two functions $f(n)$ and $g(n)$, it is not guaranteed that one of the following holds -

1. $f(n)=O(g(n))$
2. $f(n)=\Theta (g(n))$
3. $f(n)=\Omega (g(n))$

There exist functions that are incomparable under asymptotic growth. One such pair of functions is - $f(n)=n;g(n)=n^{(1+sinn)}$

Discrete Properties of Asymptotic Notations

Notation	Reflexive	Symmetric	Transitive	Transpose Symmetry
$O$	T	F	T	T
$\Omega$	T	F	T	T
$\Theta$	T	T	T	F
$o$	F	F	T	T
$\omega$	F	F	T	T

1. Reflexivity - All notations that allow equality are reflexive.
2. Symmetric - Only possible for tight bound.
3. Transitivity - Possible for all.
4. Transpose Symmetry - If $f(n)=O(g(n))$ then $g(n)=\Omega (f(n))$. Only $\Theta$ doesn’t have any such relation.