Analysis of Algorithms

Table of Contents

• Types of Analysis
  • Aposteriori Analysis
    • 1. Step Count Method
    • 2. Order of Magnitude Method
• Time Complexity
  • Cases for Time Complexity
  • Mathematical Series
    • Arithmetic Progression -
    • Geometric Progression -
    • Harmonic Progression -
    • Sum of Squares of first n Natural Numbers -
    • Sum of Cubes of first n Natural Numbers -
  • Time Complexity of Recursive functions
    • Back Substitution Method
  • Time Complexity of Loops
• Space Complexity
• Questions
  • 1. TC of Recurrence
  • 2. TC of loops
  • 3. Space Complexity

Types of Analysis

1. Aposteriori Analysis - By code execution
2. Apriori Analysis - Before code execution

Aposteriori Analysis

Two methods of Aposteriori Analysis -

1. Step Count
2. Order of Magnitude

1. Step Count Method

Counting the exact number of fundamental operations done in the code.

Example -

p = q + r                        // 2 operations
s = t * u                        // 2 operations
 
for (i=1, i<=n, i++) {           // (1 + n * 4 + 1 = 4n + 2) operations
	a = b + c
}
 
for (j=1; j<=n, j++) {           // (1 + n * (m+2) + 1) operations
	for (k=1, k<=n, k++) {       // m = 1 + n * 4 + 1 = 4n + 2 operations
		a = b + c                // Total = 4n^2 + 4n + 2 operations
	}
}

Total number of operations in the above code is - $4n^2+8n+8$.

2. Order of Magnitude Method

Instead of having the exact count, consider the order of magnitude of the fundamental statements executed.

Time Complexity

The amount of time required by any program to execute, expressed as a function of the input size is called the Time Complexity.

Cases for Time Complexity

Based upon the input there are 3 cases -

1. Best Case - Minimum number of times.
2. Worst Case - Maximum number of times.
3. Average Case - Probability dependent.

Mathematical Series

Arithmetic Progression -

$$\text{Sum of AP}=\sum _{i=1}^{n}a+i\ast d=\frac{n(2a+(n-1)d)}{2}$$

Geometric Progression -

$$\text{Sum of GP}=\sum _{i=0}^{n}a\cdot r^i=\frac{a(r^n-1)}{r-1}$$

Harmonic Progression -

$$\text{Sum of HP}=\sum _{i=1}^n\frac{1}{i}\approx logn$$

Sum of Squares of first n Natural Numbers -

$$\text{Sum of AP}=\sum _{i=1}^n{i}^2=\frac{n(n+1)(2n+1)}{6}$$

Sum of Cubes of first n Natural Numbers -

$$\text{Sum of AP}=\sum _{i=1}^n{i}^3={\left(\frac{n(n+1)}{2}\right)}^2$$

Time Complexity of Recursive functions

1. Back Substitution Method - Gives value of recurrence and TC [Universal Method]
2. Master’s Method - Works only in specific cases and only gives TC
3. Recursive Tree Approach - Only TC

Back Substitution Method

Consider the code for calculating the Factorial -

f(n) {
	if (n == 1) {
		return 1
	}
	return n * f(n-1)
}

Assume that the time complexity of f(n) is $T(n)$. We can write $T(n)$ as -

$$\begin{array}{rl}T(n)& =T(n-1)+C_1\\ T(1)& =C_2\end{array}$$

Using this information we can solve for $T(n)$ -

$$\begin{array}{rlr}T(n)& =T(n-1)+C_1& \\ & =T(n-2)+2C_1& \because T(n-1)=T(n-2)+1\\ & =T(n-3)+3C_1& \end{array}$$

This can be generalized as $T(n)=T(n-k)+k\ast C_1$. To reach the base condition we need $n-k=1$ $i.e.$ $k=n-1$.

$$\begin{array}{rl}T(n)& =T(n-(n-1))+(n-1)\ast C_1\\ & =T(1)+C_{1}n-C_1\\ & =C_{1}n-C_1+C_2\\ & =O(n)\end{array}$$

Time Complexity of Loops

The TC for any loop depends upon two factors -

1. The number of times the loop is running/iterating/repeating.
2. The complexity of all the individual statements within the loop body.

How to calculate -

1. Identify the variable(s) determining the termination criteria.
2. Identify the pattern of updation for these variables over each iteration and generalize for some $k^{th}$ iteration.
3. Calculate the iteration $k$ in terms for $n$ for which the termination criteria doesn’t satisfy. Thus the loop would run for these $k$ iterations. Check Question 4 for example.

---

Space Complexity

The amount of Auxiliary memory space (excluding the space required by the input) required by the program, expressed as a function of the input size is called the Space Complexity. Check Question 5 for example.

Questions

1. TC of Recurrence

Q1) Find the time complexity and recurrence value for -

$$\begin{array}{rlr}& T(n)=2\ast T\left(\frac{n}{2}\right)+O(n)+a& \\ & T(n)=b& [n=1]\end{array}$$

where $a$ and $b$ are constants and $n$ is the input size.

Sol${}^n$ - Since $O(n)$ dominates the constant $a$, we can simplify $T(n)$ to be -

$$\begin{array}{rl}T(n)& =2\ast T\left(\frac{n}{2}\right)+n\\ T\left(\frac{n}{2}\right)& =2\ast T\left(\frac{n}{4}\right)+\frac{n}{2}\end{array}\text{\hspace{1em}(1)(2)}$$ $$\begin{array}{rlrlrl}T(n)& =4T\left(\frac{n}{4}\right)+2n& & \because & & \text{Using (2)}\\ & =8T\left(\frac{n}{8}\right)+3n& & \because & & \text{Substituting }T\left(\frac{n}{4}\right)\\ & =2^{3}T\left(\frac{n}{2^3}\right)+3n& & & & \\ & =2^{k}T\left(\frac{n}{2^k}\right)+kn& & & & \text{Generalising for some}{k}^{th}term\end{array}\text{\hspace{1em}(3)}$$

For what value of $k$ would be achieve the base case of $n=1$?

$$\begin{array}{rl}\frac{n}{2^k}& =1\\ \Rightarrow n& =2^k\\ \Rightarrow k& =\log n\end{array}$$

Putting $k=logn$ and $n=2^k$ in $(3)$,

$$\begin{array}{rl}T(n)& =2^{k}T\left(\frac{n}{2^k}\right)+kn\\ & =nT(1)+nlogn\\ & =bn+nlogn\\ & =\boxed{O(nlogn)}\end{array}$$

---

Q2) Find the worst case and best case time complexity for the below diagram

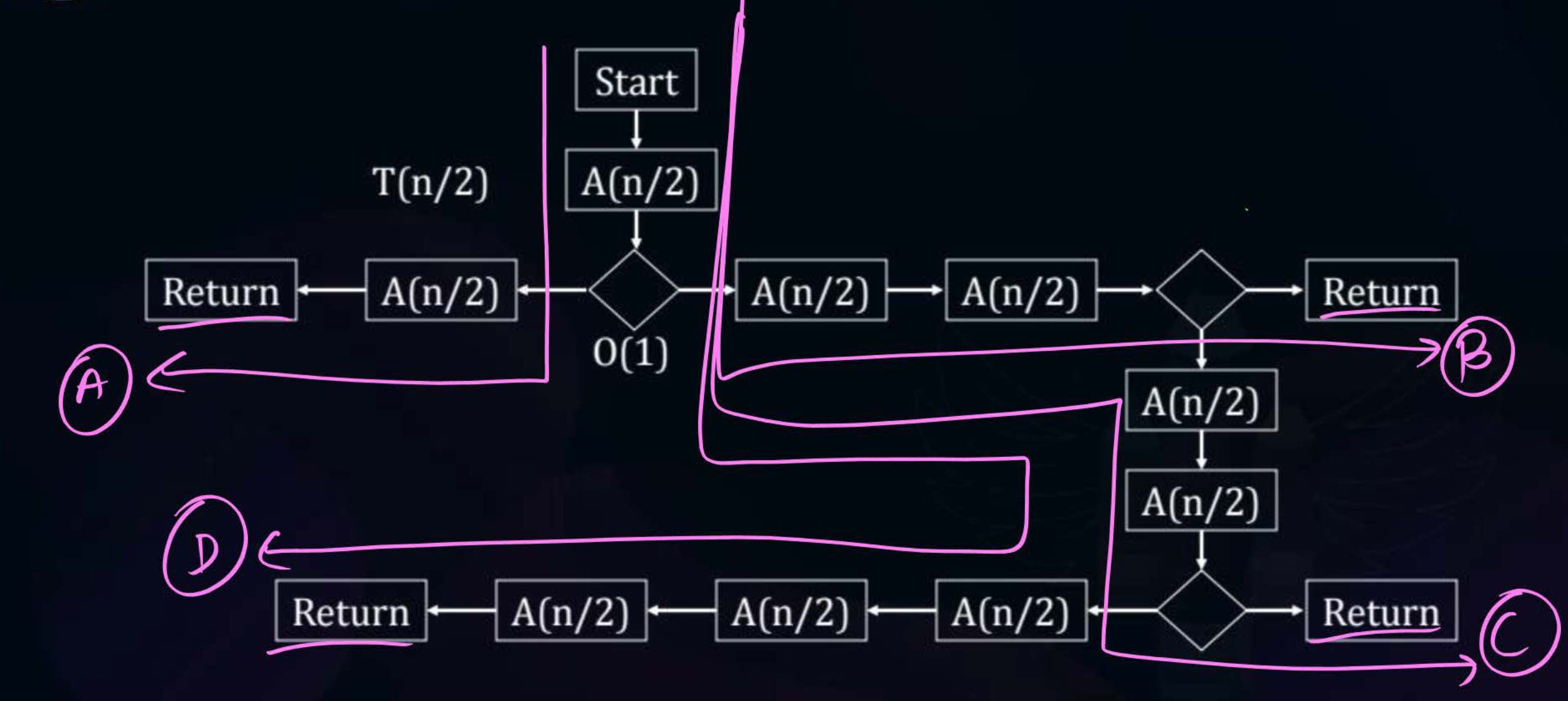
Sol${}^n$ - Best Case TC is achieved by Path A - $O(n)$ Worst Case TC is achieved by Path A - $O(n^3)$

---

2. TC of loops

Q3) Find the TC of the below code -

i = 1, a = 0;
while (i = 2) {
	a += 1;
}

Sol${}^n$ - The condition i=2 is not a comparison but an assignment. Thus the loop’s condition is always true and this runs infinitely.

---

Q4) Find the TC of the below code -

Sol${}^n$ -

$$\begin{array}{rl}& 1^{st}\text{Iteration}-b=2;a=1+2;\\ & 2^{nd}\text{Iteration}-b=3;a=1+2+3;\\ & 3^{rd}\text{Iteration}-b=4;a=1+2+3+4;\\ & ⋮\\ & k^{th}\text{Iteration}-b=k+1;a=1+2+\cdots +k+1=\frac{(k+1)(k+2)}{2};\end{array}$$

For the loop to terminate $a>n$, so $a=n$ will be cause the last iteration.

$$\begin{array}{rlrl}& & \frac{(k+1)(k+2)}{2}& =n\\ & \Rightarrow & \frac{k^2}{2}& \approx n\\ & \Rightarrow & k^2& \approx 2n\\ & \Rightarrow & k& \approx \boxed{\sqrt{n}}\end{array}$$

Thus the loop would run for $k=\sqrt{n}$ iterations. Thus TC = $O(\sqrt{n})$

---

3. Space Complexity

Q5) Find the SC of the below code -

Sol${}^n$ - The elements that would be added to the recursion stack would be - $n,\frac{n}{2},\frac{n}{4},\frac{n}{8},\dots ,\frac{n}{2^{k-1}},\dots ,1$. The total number of elements would be -

$$\begin{array}{rlrl}& & \frac{n}{2^{k-1}}& =1\\ & \Rightarrow & n& =2^{k-1}\\ & \Rightarrow & k-1& =lo{g}_{2}n\\ & \Rightarrow & k& \approx \boxed{lo{g}_{2}n}\end{array}$$

Thus the Space Complexity is $O(logn)$.