Formulas

In addition to these, also see the Mathematical Series discussed in Analysis of Algorithms.

Permutations -

^{n} P_{r} = \frac{n !}{( n - r )!}

Combinations (Repetition not allowed) -

^{n} C_{r} = \frac{^{n} P _{r}}{r !} = \frac{n !}{r ! ( n - r )!}

Combinations (Repetition allowed), bars and stars example in Question 2 -

= (r - 1 n + r - 1) = \frac{( n + r - 1 )!}{n ! ( r - 1 )!}

Pascal’s rule -

^{n} C_{r} = (r n) = (r n - 1) + (r - 1 n - 1)

Q1) Find a formula for counting the number of diagonals in an n-gon

Sol $^{n}$ - The $n$ vertices can be connected using a line in $^{n} C_{2}$ ways. Out of these connections, $n$ connections would be edges connecting adjacent vertices. Thus the number of diagonals is $^{n} C_{2} - n$ .

Q2) A shopkeeper has 3 ice-cream flavors. In how many ways can he sell these flavors to 10 kids

Sol $^{n}$ - Consider 12 slots and 2 sticks. These 2 sticks can be used to divide the 12 slots into 3 sections like this -

So now the problem has shifted to picking 2 slots from 12 total slots to insert the sticks in. Thus the answer is $^{12} C_{2} = 66$ . A more general solution to this would be $(r - 1 n + r - 1)$ where $n$ is the number of children and $r$ is the number of flavors.

Q3) In how many ways can we write 100 as a sum of 4 non-negative integers.

Sol $^{n}$ - This can be modelled as a similar problem with 103 slots and 3 sticks. Thus the solution is $(3 103) = \frac{103 !}{100 ! \cdot 3 !} = \frac{101 * 102 * 103}{6} = 176, 851$

Binomial Theorem

In the expansion of $(a + b)^{n}$ , each term is of the form $a^{x} b^{y}$ where $0 \leq x \leq n$ and $y = n - x$ . For any term $a^{x} b^{y}$ , $a$ must have been contributed by $x$ number of $(a + b)$ terms while the rest $n - x$ number of terms contributed towards $b$ . We can choose $x$ of the $n$ factors from which $a$ is selected in $^{n} C_{x}$ ways. Thus the coefficient of any term $a^{x} b^{n - x}$ is $^{n} C_{x}$ .

(a + b)^{n} = i = 0 \sum n (n - i n) \cdot a^{n - i} b^{i} = a^{n} + (n - 1 n) a^{n - 1} b + \dots + (1 n) a b^{n - 1} + b^{n}

Interesting Applications

Euler’s constant - $n \to \infty lim (1 + \frac{1}{n})^{n} = k = 0 \sum \infty \frac{1}{k !}$
Derivative of $x^{n}$ $\frac{d}{d x} x^{n} = n \to \infty lim \frac{x ^{n + h} - x ^{n}}{h} = n \cdot x^{n - 1}$
We know $(a + b)^{n} = \sum_{i = 0}^{n} (n - i n) \cdot a^{n - i} b^{i}$ . What if $a = b = 1$ ?

(1 + 1)^{n} Thus, 2^{n} = i = 0 \sum n (n - i n) \cdot 1^{n - i} 1^{i} = i = 0 \sum n (n - i n) \cdot 1 = (0 n) + (1 n) + (2 n) + \dots + (n n) = (0 n) + (1 n) + (2 n) + \dots + (n n)

Using a similar logic we can find -

(1 - 1)^{n} \Rightarrow (2 n) + (4 n) + (6 n) + \dots = (1 n) - (2 n) + (3 n) - (4 n) + \dots = (1 n) + (3 n) + (5 n) + \dots

Extended binomial coefficient - For any real number $r$ , the binomial coefficient is defined by $(k r) = \frac{r ( r - 1 ) ( r - 2 ) \dots ( r - k + 1 )}{k !}$ . Now let $n \in N$ and substitute $r = - n$ . Then,

(k - n) = \frac{( - n ) ( - n - 1 ) ( - n - 2 ) \dots ( - n - k + 1 )}{k !} = \frac{( - 1 ) ^{k} n ( n + 1 ) ( n + 2 ) \dots ( n + k - 1 )}{k !} = (- 1)^{k} \frac{( n + k - 1 )!}{k ! * ( n - 1 )!} = (- 1)^{k} (k n + k - 1)

- Using this we can find -

\frac{1}{1 - x} \frac{1}{1 + x} = 1 + x + x^{2} + x^{3} + x^{4} \dots = 1 - x + x^{2} - x^{3} + x^{4} \dots

$r^{t h}$ term of the Binomial Expansion

The $r^{t h}$ term of the Binomial Expansion is always - $(r - 1 ! n) a^{n - r + 1} b^{r - 1}$

Multinomial Theorem

What would the coefficients of each term look like in the expansion of $(a + b + c + \dots)^{n}$ ?

We can consider $(a + b + c + \dots)^{n} = (a + R_{1})^{n}$ where $R_{1} = (b + c + \dots)$ . Upon expansion by applying the binomial theorem, any $(n_{1} + 1)^{t h}$ term (for simpler calculations without loss of generalization) would be of the form -

(n _{1} n) a^{n_{1}} R_{1}^{n - n_{1}}

$R_{1}^{n - n_{1}} = (b + R_{2})^{n - n_{1}}$ where $R_{2} = (c + \dots)$ . The coefficient of some $(n_{2} + 1)^{t h}$ term of this expansion would be -

(n _{2} n - n _{1})

We can continue doing this expansion until $R_{k}$ becomes a binomial. By that point, the coefficient of the $(n_{1} + 1)^{t h}$ of the original multinomial would be -

(n _{1} n) \cdot (n _{2} n - n _{1}) \cdot (n _{3} n - n _{1} - n _{2}) \dots (n _{k} n - n _{1} - n _{2} \dots - n _{k - 1})

= \frac{n !}{n _{1} ! \cdot ( n - n _{1} )!} \cdot \frac{( n - n _{1} )!}{n _{2} ! \cdot ( n - n _{1} - n _{2} )!} \dots \frac{( n - n _{1} - n _{2} \dots - n _{k - 1} )!}{n _{k} ! \cdot ( n - n _{1} - n _{2} \dots - n _{k} )!} = \frac{n !}{n _{1} ! \cdot ( n - n _{1} )!} \cdot \frac{( n - n _{1} )!}{n _{2} ! \cdot ( n - n _{1} - n _{2} )!} \dots \frac{( n - n _{1} - n _{2} \dots - n _{k - 1} )!}{n _{k} ! \cdot ( n - n _{1} - n _{2} \dots - n _{k} )!} = \frac{n !}{n _{1} ! \cdot n _{2} ! \dots n _{k} !}

Pascal’s Triangle

Each row $i$ of the Pascal’s Triangle contains the Binomial Coefficients of the expansion $(a + b)^{i}$ .

Fun Facts

The second diagonal is the sequence of Natural Numbers.
Each $i^{t h}$ row’s sum is $2^{i - 1}$ .
Each row also denotes $1 1^{i - 1}$ .

Catalan’s Numbers

In how many ways can one reach $(5, 5)$ from $(0, 0)$ in the below $5 \times 5$ grid?

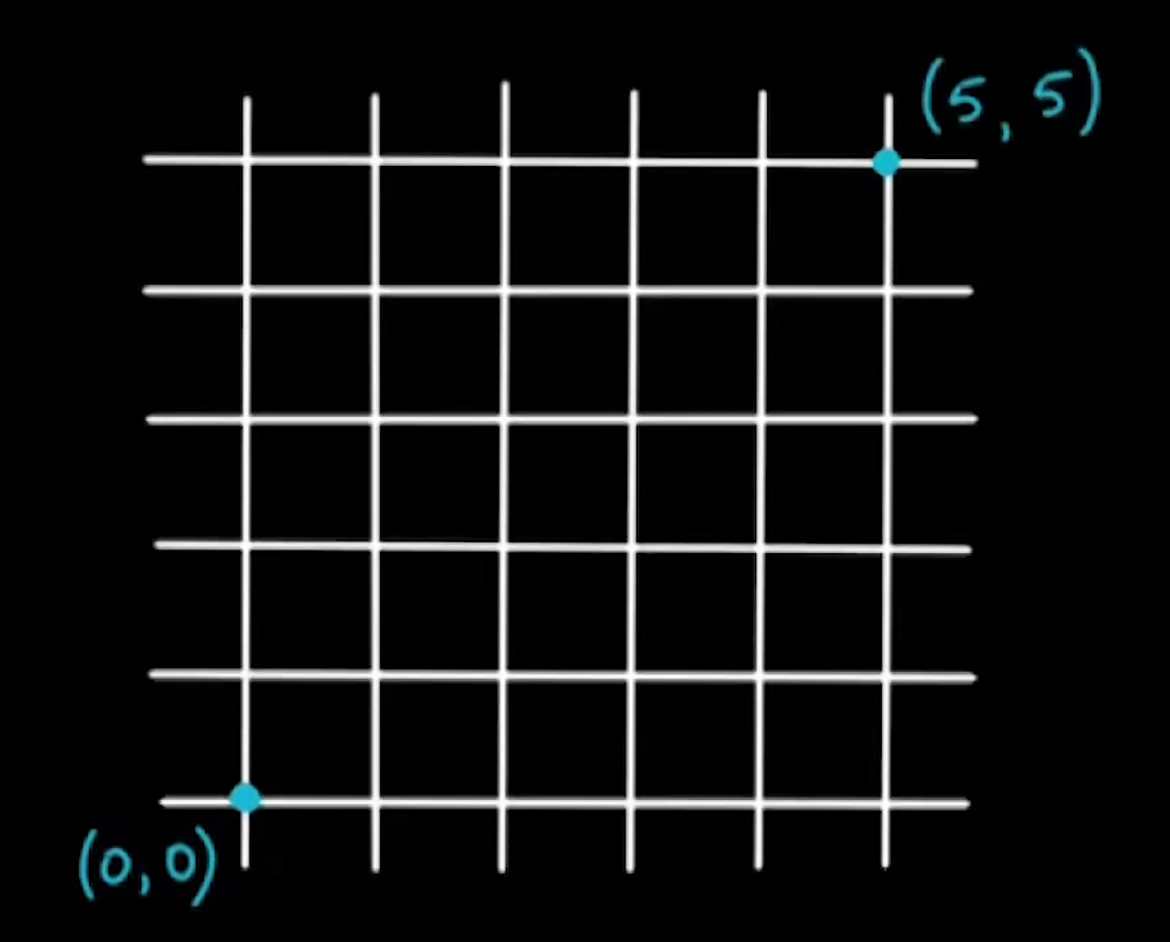
Pigeon Hole Principle

The principle states that if we have $m$ pigeons and $n$ pigeon holes such that $m > n$ . Then there would at least be one pigeon hole such that at least 2 pigeons reside in it.

Usually used in finding the worst case of the number of item pickings such that it satisfied some constraint.

Sol $^{n}$ - There are a total of 26 letter in the English Alphabets. So a person’s initial can be - A.A., A.B., A.C., $\dots$ , Z.Z. Only after all $2 6^{2}$ initials have been covered can we say that seating one more person will ensure that at least two people share the same initials. Thus the number of pigeon holes we have is $2 6^{2}$ and the number of “pigeons” or minimum number of people needed is $2 6^{2} + 1$ .

Generating Function

The idea of a generating function is if you have some question with the answer associated with some positive integer, you can model the problem as a polynomial such that the coefficients of certain terms would correspond to this answer.

Say we want the number of subsets of ${1, 2, 3, 4}$ such that the sum of the elements in each subset is equal to 5. We can model this as a polynomial problem of $f (x) = (1 + x) (1 + x^{2}) (1 + x^{3}) (1 + x^{4})$ such that the coefficient corresponding to $x^{5}$ in the product would be this count. Here $f (x)$ is your generating function.

No idea how someone thought of this (even 3Blue1Brown doesn’t) but it can be seen why the above example would work. A generating function is of the form -

G (x) = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + \dots = i = 0 \sum n a_{i} x^{i}

Recurrence Relation

Back Substitution is discussed in Analysis of Algorithms, so only method of characteristic roots will be discussed here.

GATE & BS Notes

Explorer

Counting

Formulas

Q1) Find a formula for counting the number of diagonals in an n-gon

Q2) A shopkeeper has 3 ice-cream flavors. In how many ways can he sell these flavors to 10 kids

Q3) In how many ways can we write 100 as a sum of 4 non-negative integers.

Binomial Theorem

Interesting Applications

$r^{t h}$ term of the Binomial Expansion

Multinomial Theorem

Pascal’s Triangle

Fun Facts

Catalan’s Numbers

Pigeon Hole Principle

Generating Function

Recurrence Relation

Method of characteristic roots

Graph View

Table of Contents

Backlinks

GATE & BS Notes

Explorer

Counting

Formulas

Q1) Find a formula for counting the number of diagonals in an n-gon

Q2) A shopkeeper has 3 ice-cream flavors. In how many ways can he sell these flavors to 10 kids

Q3) In how many ways can we write 100 as a sum of 4 non-negative integers.

Binomial Theorem

Interesting Applications

rth term of the Binomial Expansion

Multinomial Theorem

Pascal’s Triangle

Fun Facts

Catalan’s Numbers

Pigeon Hole Principle

Q4) What is the minimum number of ways people can be seated in a hall such that it always ensures that at least two people share the same first name and last name initials.

Generating Function

Recurrence Relation

Method of characteristic roots

Graph View

Table of Contents

Backlinks

$r^{t h}$ term of the Binomial Expansion