Trees

Table of Contents

• Binary Tree
• Properties of binary trees
  • Number of Binary Trees Possible
• Tree Traversal
  • Breadth First Traversal
  • Depth First Traversal
    • Pre-Order Traversal
    • In-Order Traversal
    • Post-Order Traversal
• Binary Search Tree
  • Deletion of a node in a B.S.T
    • Deleting a leaf node
    • Deleting an internal node with one child
    • Deleting an internal node with two children
• Array representation of Binary Tree
• Binary Heap
  • Insertion in a Binary Heap
  • Deletion in a Binary Heap
  • Number of distinct Binary Heaps possible
• AVL Tree
  • Balancing a B.S.T
    • LL Rotation
    • RR Rotation
    • LR Rotation
    • RL Rotation

A tree is a non-linear data structure in which elements are stored as nodes and connected in a hierarchical manner.

Some important terminologies for a tree are -

1. Nodes - Elements in a tree.
2. Edges - Connections between nodes.
3. Root Node - The topmost node in the tree.
4. Left/Terminal/External Node - The bottom most nodes in the tree with no children.
5. Internal Node - Any node in the tree which has at least one child.
6. Sibling Nodes - Nodes with a common parent.
7. Degree of a node - The number of children of that node.
8. Degree of the tree - The maximum degree of all nodes in the tree.
9. Level - The distance of the node from the root node (convention dependent, most books have root node as level 0 but some as level 1).
10. Depth - The number of edges from the root to that node (convention independent, root node is always at depth 0).
11. Height - The length of longest path from the node to a leaf node.
12. Height of the tree - The maximum height of all nodes in the tree.

Binary Tree

A tree with each node having a degree $\le$ 2.

Types of Binary trees -

1. Full Binary Tree - Every node must have a degree of either 0 or 2.
2. Complete Binary Tree - All levels except the last level of the tree must be completely filled (each level except the last has $2^n$ nodes) and nodes are filled from top to bottom and left to right.
3. Perfect Binary Tree - Every level of the tree must be completely filled (each level has $2^n$ nodes).
4. Skewed Binary Tree - All nodes except leaf nodes must have a degree of 1 and all children must be the left child or the right child.
5. Degenerate Binary Tree - All nodes except leaf nodes must have a degree of 1 and but children can either be a left child or a right child.

Properties of binary trees

1. Number of edges in a binary tree - $n-1$ ($n$ is the number of nodes).
2. Number of external nodes in an F.B.T - $i+1$ ($i$ is the number of internal nodes).
3. Similarly, total number of nodes in an F.B.T or P.B.T - $2\ast i+1$ ($i$ is the number of internal nodes).
4. In a binary tree, if there are $l$ leaf nodes then the number of nodes with degree $2$ are - $l-1$.
5. A binary tree of height $H$ can be made using -
   1. Minimum no. of nodes - $H+1$
   2. Maximum no. of nodes - $2^{H+1}-1$
6. Using the above property, we can say that with $n$ nodes we can have -
   1. Minimum height - $lo{g}_2(N+1)-1$
   2. Maximum height - $N-1$

Number of Binary Trees Possible

1. The number of unlabeled binary trees that can be formed using $n$ nodes is the Catalan’s Numbers formula - $\frac{{}^{2n}{C}_n}{n+1}$.
2. The number of labeled binary trees that can be formed using $n$ nodes is - $n!\ast \frac{{}^{2n}{C}_n}{n+1}$.

Tree Traversal

Breadth First Traversal

Also known as Level Order Traversal. Each level of a tree is covered before moving to the next level.

Depth First Traversal

Pre-Order Traversal

The tree is traversed depth wise manner from left to right. Only when a leaf node is reached, we backtrack to the parent and start exploring the other children.

• If the node is an internal node, only note it down if it is visited the first time during depth first traversal, else ignore.
• If the node if a leaf node, note it down regardless of how many times it has been visited.

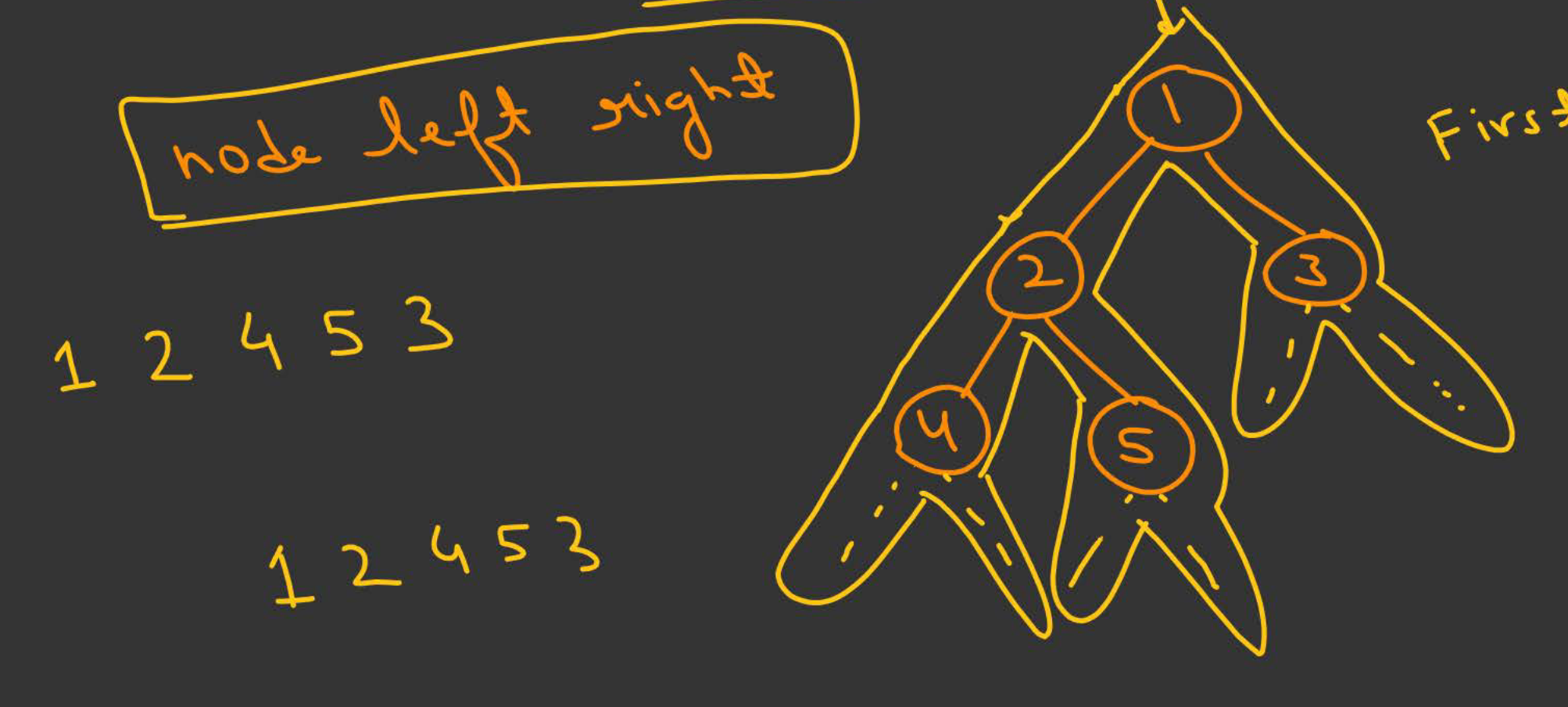
In-Order Traversal

The tree is again traversed in a depth wise manner from left to right. But a node is traversed only after its left subtree is traversed.

• If the node is an internal node, only note it down if it is visited the second time during depth first traversal, else ignore.
• If the node if a leaf node, note it down regardless of how many times it has been visited.

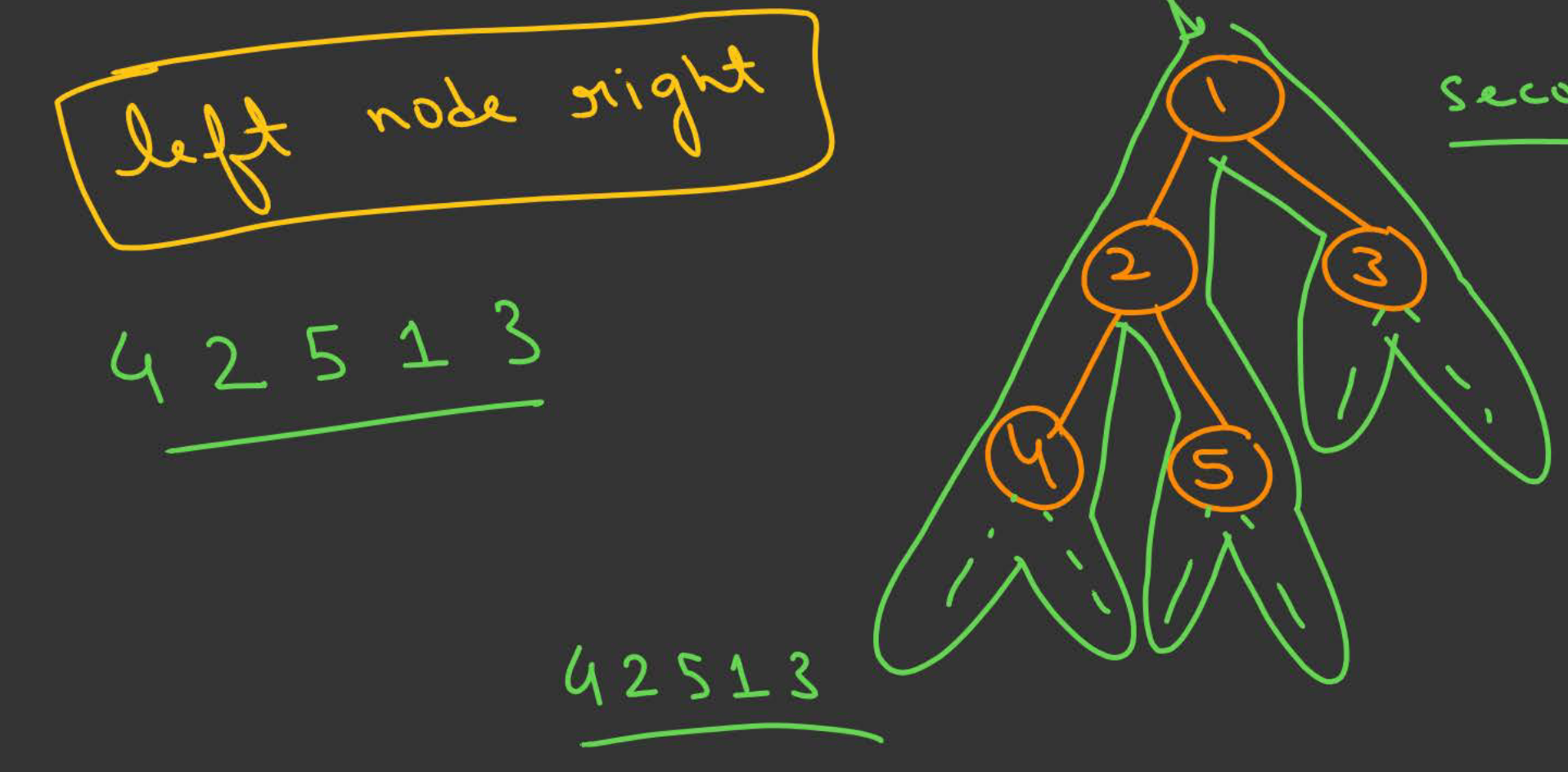
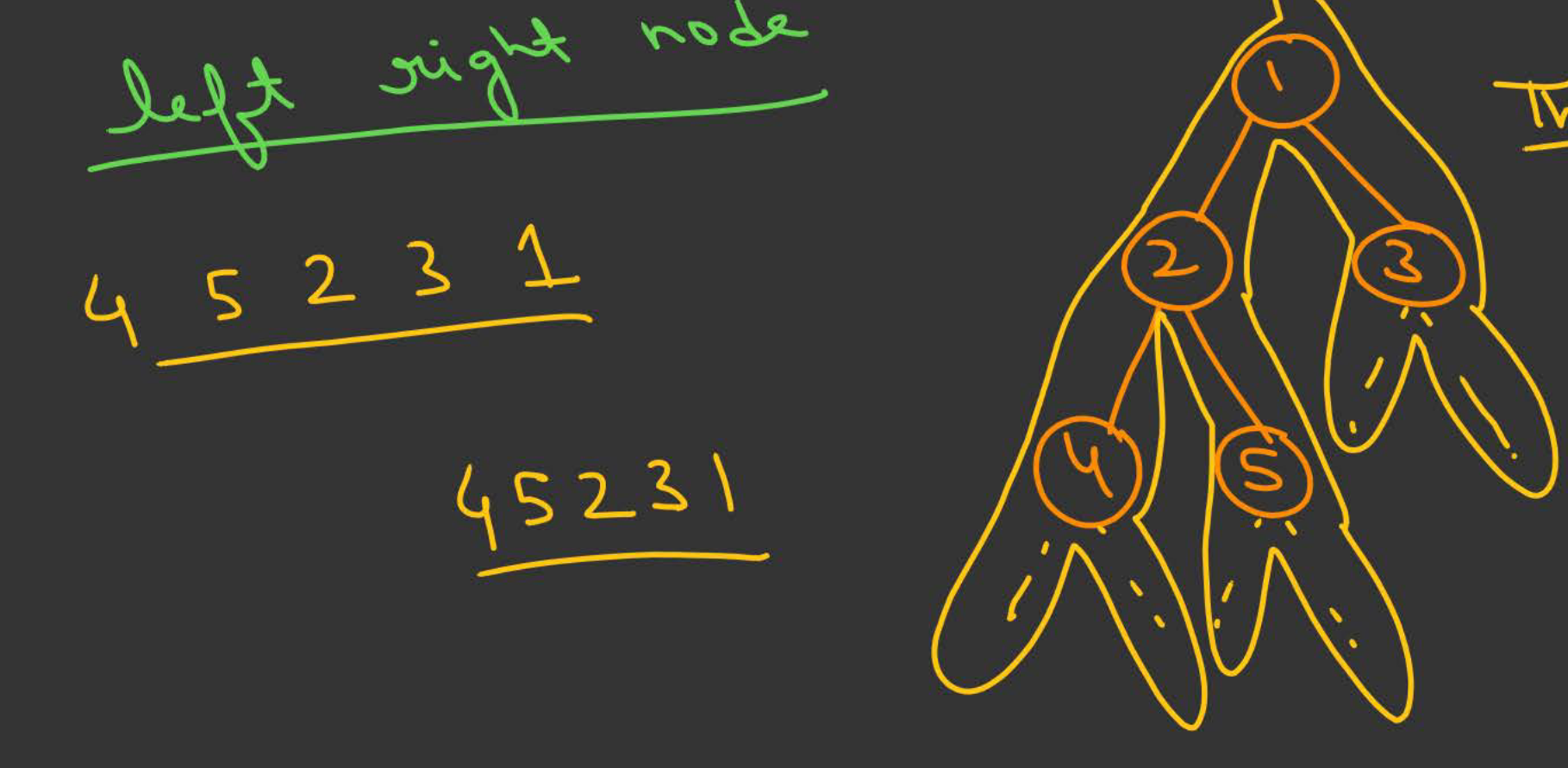
Post-Order Traversal

The tree is again traversed in a depth wise manner from left to right. But a node is traversed only after its left subtree and right subtree are traversed.

• If the node is an internal node, only note it down if it is visited the third time during depth first traversal, else ignore.
• If the node if a leaf node, note it down regardless of how many times it has been visited.

Binary Search Tree

A tree in which the left subtree nodes $<$ parent node $<$ right subtree nodes.

• The in-order traversal of a B.S.T will always give the values of the B.S.T in ascending order.
• For inserting an element to a non-perfect B.S.T of $n$ nodes -
  • Best Case Time Complexity - $O(1)$ (When the tree is empty or insertion happens at the root)
  • Worst Case Time Complexity - $O(n)$ (When the BST is completely skewed)

Time Complexities

1. Time Complexity of merging two BSTs is $\Theta (n+m)$.
2. Using Build Heap, can be converted into a Heap in $\Theta (n)$.

Deletion of a node in a B.S.T

There are three cases possible for this

Deleting a leaf node

If the node to delete is a leaf node, just identify the parent of that node using tree traversal and remove the pointer to the leaf from the parent.

Deleting an internal node with one child

If the node to delete is an internal node with only one child, first identify the parent of that node using tree traversal. In the parent, replace the pointer to the internal node with the pointer to the internal node’s left/right child.

Deleting an internal node with two children

If the node $n$ to delete is an internal node with two children then -

• Swap the node with its in-order successor (default)
• Swap the node with its in-order predecessor

Steps -

1. Identify the in-order predecessor/successor to that node by first listing all nodes in an in-order manner. Let this node be some $m$.
2. Swap the internal node with $m$.
3. Delete $m$. If $m$ is a leaf node or an internal node with one child, the deletion is straight forward. If $m$ is also an internal node with two children, execute Step 1 but this time w.r.t $m$. If the B.S.T is a finite B.S.T, one such swapping will eventually result in a predecessor/successor which is either a leaf or only has one child.

Array representation of Binary Tree

The convention for an array representation of a Binary Tree is to add elements of an array in a breadth-first manner.

The below tree can be represented as -

tree = [60, 50, 70, 10, 100, 90, None, 1, 2, None, None, None, None]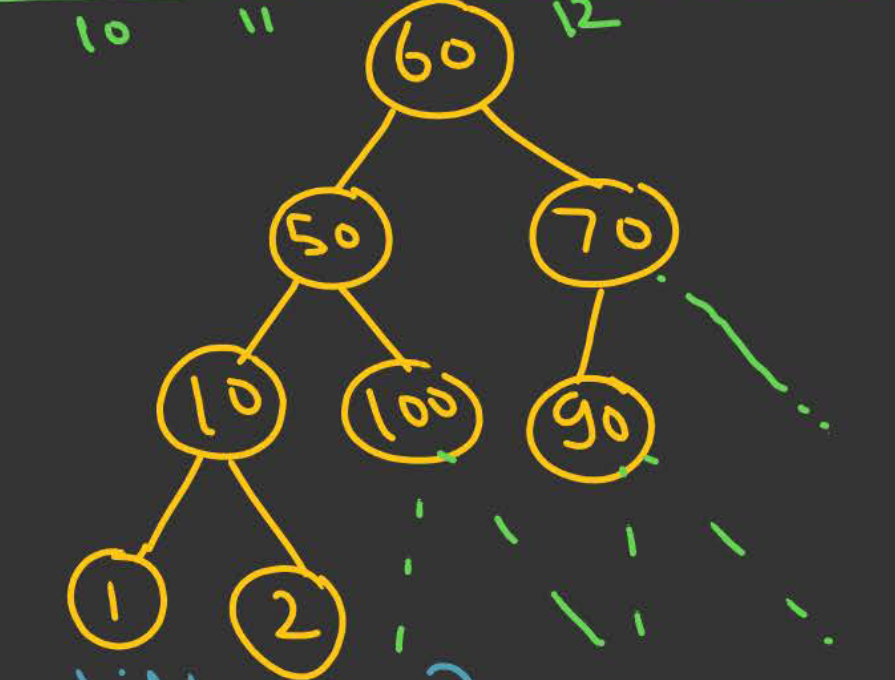

None is used to represent the lack of a child node in the leaf level for certain internal nodes.

Properties -

1. Left child of any node at index $i$ is at – $2i+1$
2. Right child of any node at index $i$ is at – $2i+2$
3. Left children are at odd indices.
4. Right children are at even indices.

Binary Heap

A Binary Heap is what powers a Priority Queue. A Binary Tree is a Binary Heap if -

1. Shape Property - The tree should be a complete Binary Tree.
2. Ordering Property - All parent nodes in the tree should either be greater than all of its children or smaller than all of its children.
   1. If parent $\ge$ all children $\to$ Max Heap
   2. If parent $\le$ all children $\to$ Min Heap

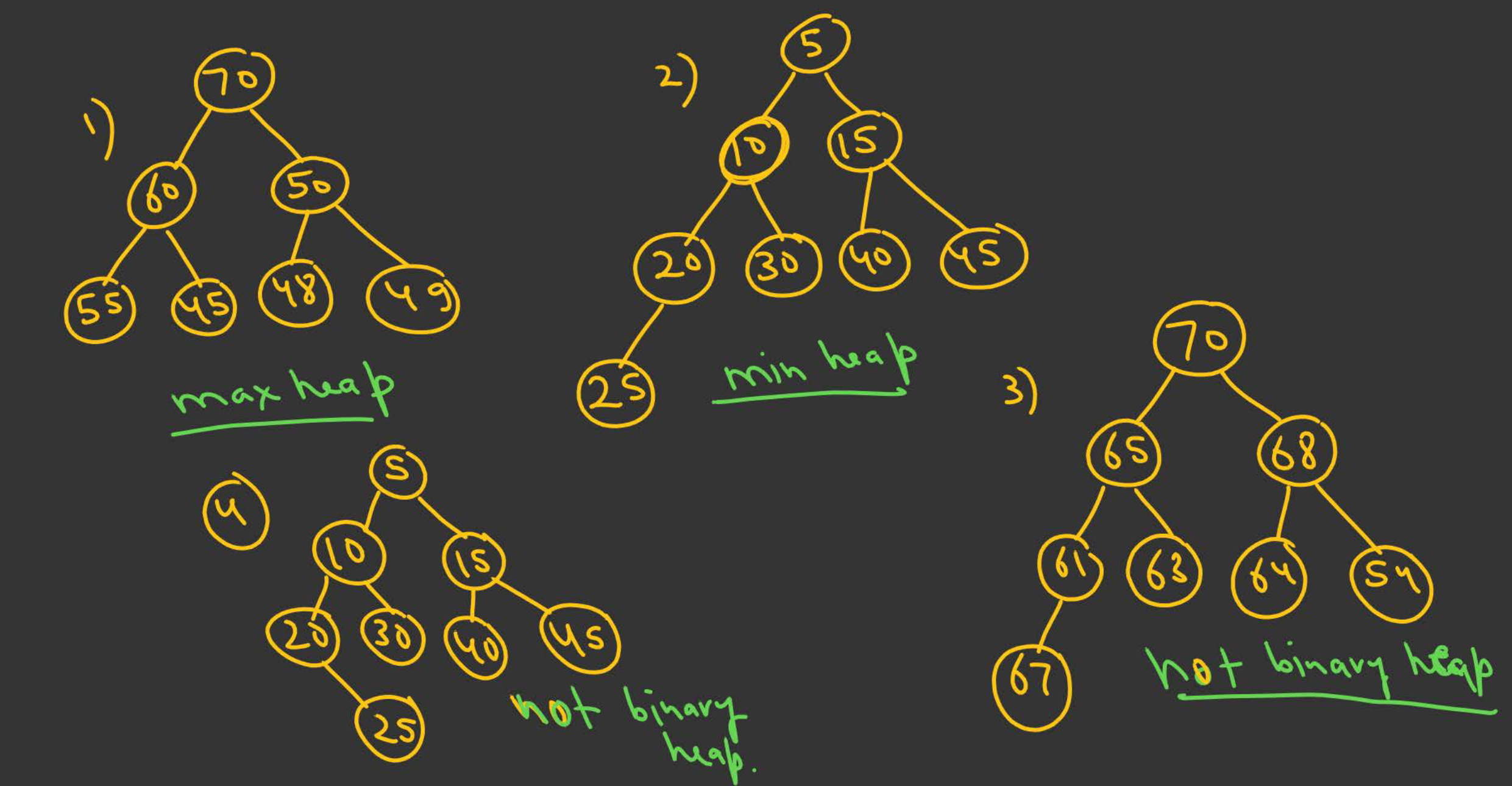
In the above image -

1. 1 is a Max Heap because it satisfied both the Shape and Ordering Property of a heap.
2. 2 is a Min Heap because it satisfied both the Shape and Ordering Property of a heap.
3. 3 is not a heap because it fails the Ordering Property of a Max heap because 61 $\le$ 67.
4. 4 is not a heap because it fails the Shape Property of a heap because 4 is not a Complete Binary Tree as 25 is on the right of 20 even though 20 has no left child. In a Complete Binary Tree the nodes need to be entered from a top-down and left-right manner.

Heap Sort is a side effect of the Ordering Property of the heap data-structure.

Time Complexities

1. In worst case, Heap building requires $\Theta (nlogn)$ time.
2. If given a sorted array of elements, using the Build Heap method a new heap can be made in $\Theta (n)$ time.
3. Time Complexity of merging two heaps is $\Theta (n+m)$.

Insertion in a Binary Heap

To insert a new item in the Binary Heap, a node node needs to be added to the Heap Tree -

1. Identify where the new node goes such that the Shape Property of the Heap is maintained. Insert the new element as a leaf node to this tree.
2. Heapify - Now to satisfy the Ordering Property of the Heap, check whether the new node and its parent follow the Ordering Property. If they don’t then keep swapping the node with its parent until the Ordering Property is satisfied.

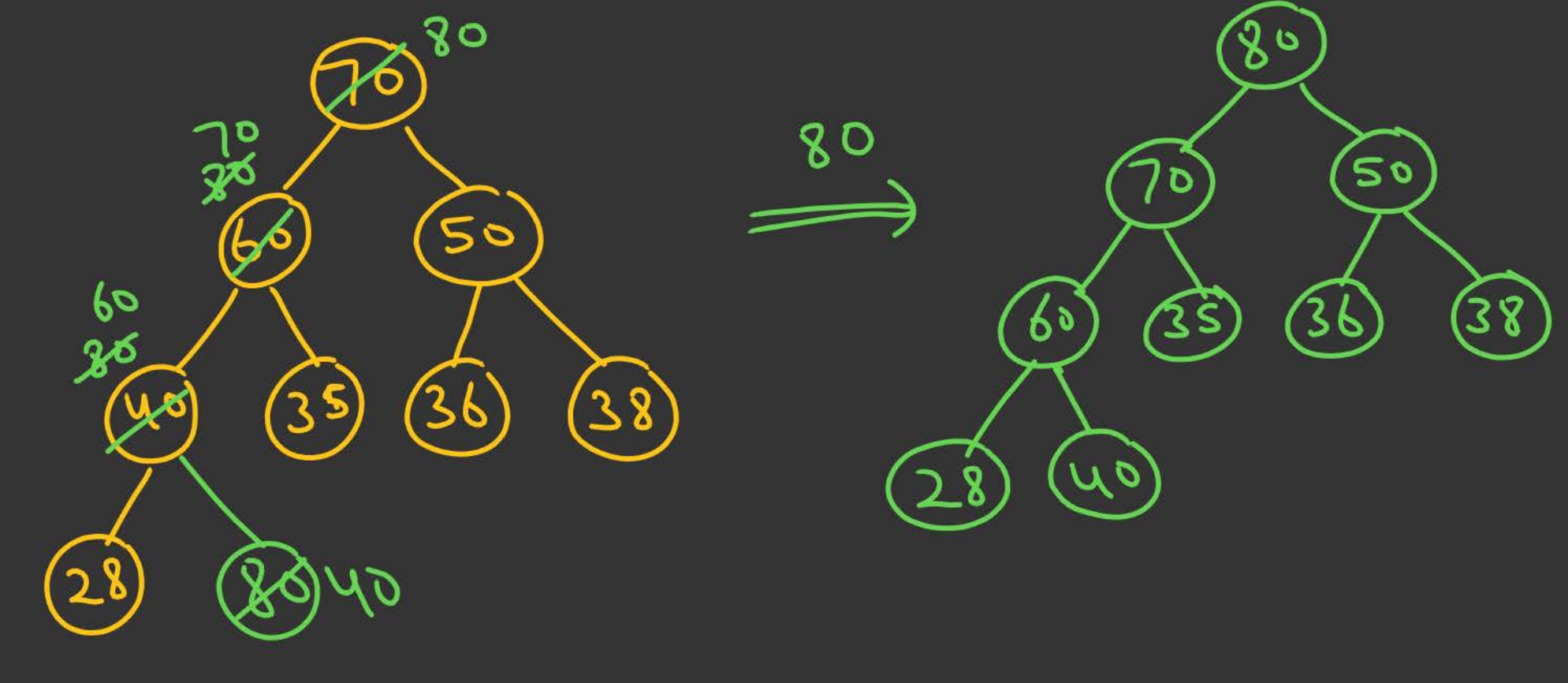
A Binary Heap can be constructed from scratch by just following these insertion rules. Worst case time complexity is $O(logn)$.

Deletion in a Binary Heap

Deletion in a Binary Heap is always done on a priority basis, meaning that in a Max Heap the current maximum element is deleted while in a Min Heap the current minimum element is deleted.

1. Swap the root node with the last leaf node in the heap and delete the leaf node.
2. As now a leaf node is at the root of the heap, call heapify from the root to satisfy the Heap Invariant.
   1. During this heapify a case can occur where the root fails the Heap Invariant with both its children. In such a case pick the child that has a higher priority than the other and swap it with the root.
   2. If the root fails the Heap Invariant with only one of the children, swap the root and the child.

Worst case complexity - $O(logn)$

Number of distinct Binary Heaps possible

The number of distinct Binary Heaps possible for $n$ elements is -

$$T(n)=\left(\genfrac{}{}{0ex}{}{n-1}{L}\right)\ast T(L)\ast T(n-1-L)$$

Reasoning -

• In a Min/Max heap only one element can go to the root. Rest $n-1$ elements must be chosen such that they satisfy the Shape Property of a Binary Heap.
• Let $L$ be the number of elements chosen from $n$ elements to be in the left subtree of the root and let $R$ be the number of elements chosen to be in the right subtree of the root.
• Only one combination of variables $L$ and $R$ can satisfy this Shape Property while also satisfying the constraint that $L+R=n-1$.

AVL Tree

A height balanced B.S.T is called an AVL Tree.

• A tree is said to be height balanced if the balancing factor for each node is in the range of $\{-1,0,1\}$.
• Balancing Factor = Height of left sub-tree - Height of right sub-tree. Balancing factor for leaf nodes is 0.

Balancing a B.S.T

To balance a given B.S.T we can perform rotations -

1. Single Rotation -
   • LL Rotation
   • RR Rotation
2. Double Rotation -
   • LR Rotation
   • RL Rotation

Critical Node - Any node with a balancing factor that doesn’t belong to the allowed range of $\{-1,0,1\}$.

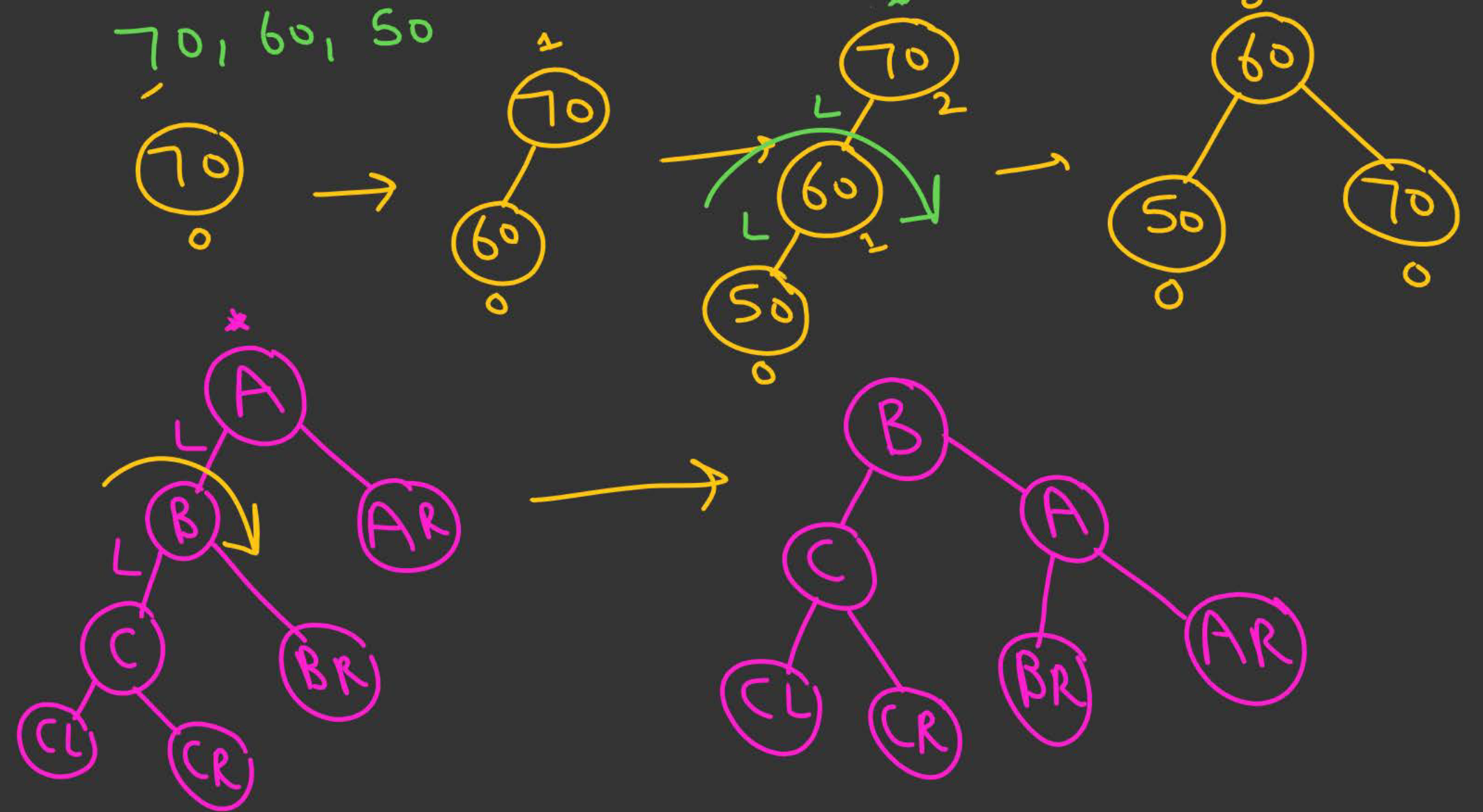
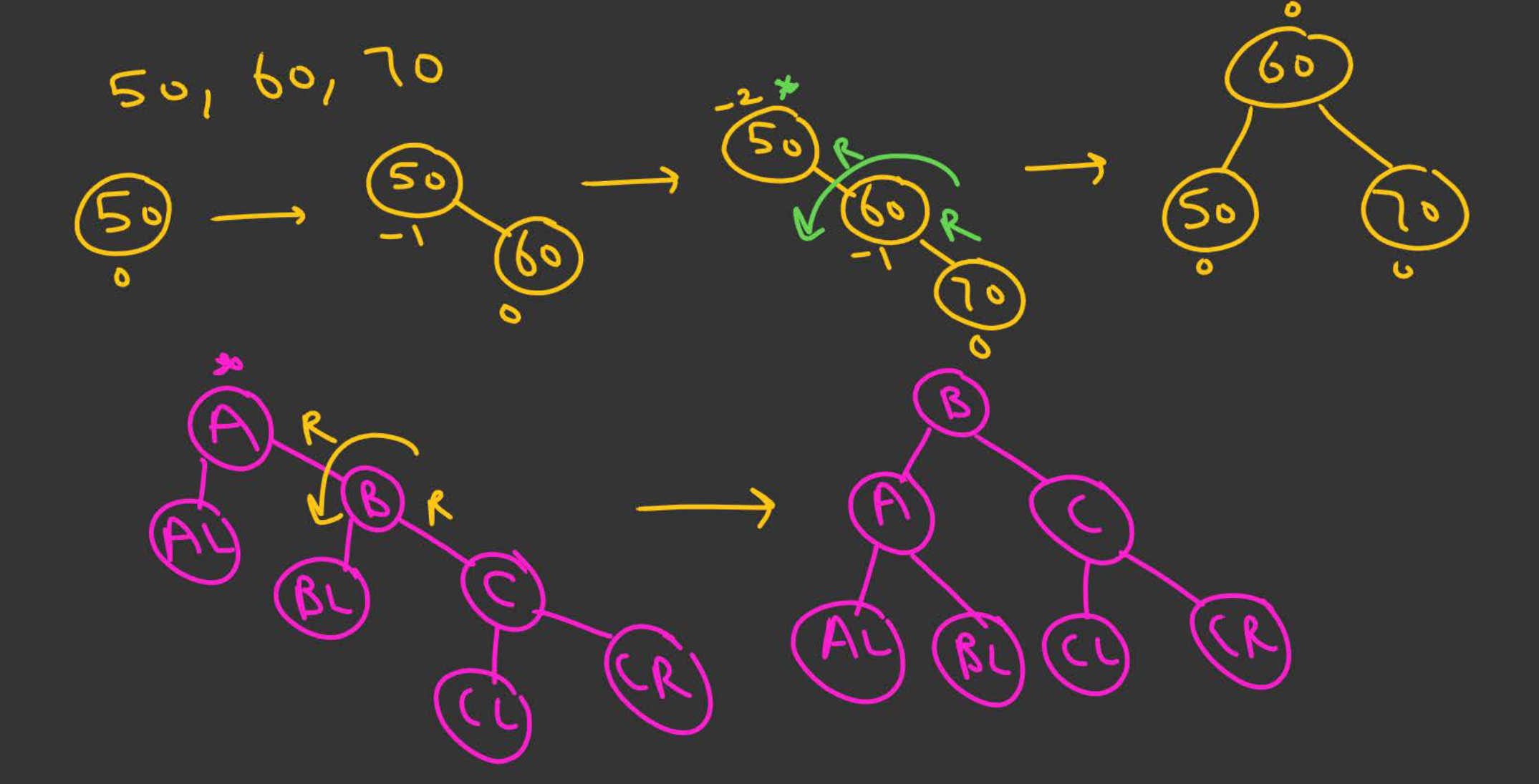
LL Rotation

Done when insertion of a new node happens in the left subtree of the left child of a critical node.

• Let A be the first critical node from the bottom.
• Let B be A’s left child.
• Perform a single right rotation:
  • B becomes the new root of this subtree.
  • A becomes the right child of B.
  • B’s right subtree becomes A’s left subtree.

RR Rotation

Done when insertion of a new node happens in the right subtree of the right child of a critical node.

• Let A be the first critical node from the bottom.
• Let B be A’s right child.
• Perform a single left rotation:
  • B becomes the new root of this subtree.
  • A becomes the left child of B.
  • B’s left subtree becomes A’s right subtree.

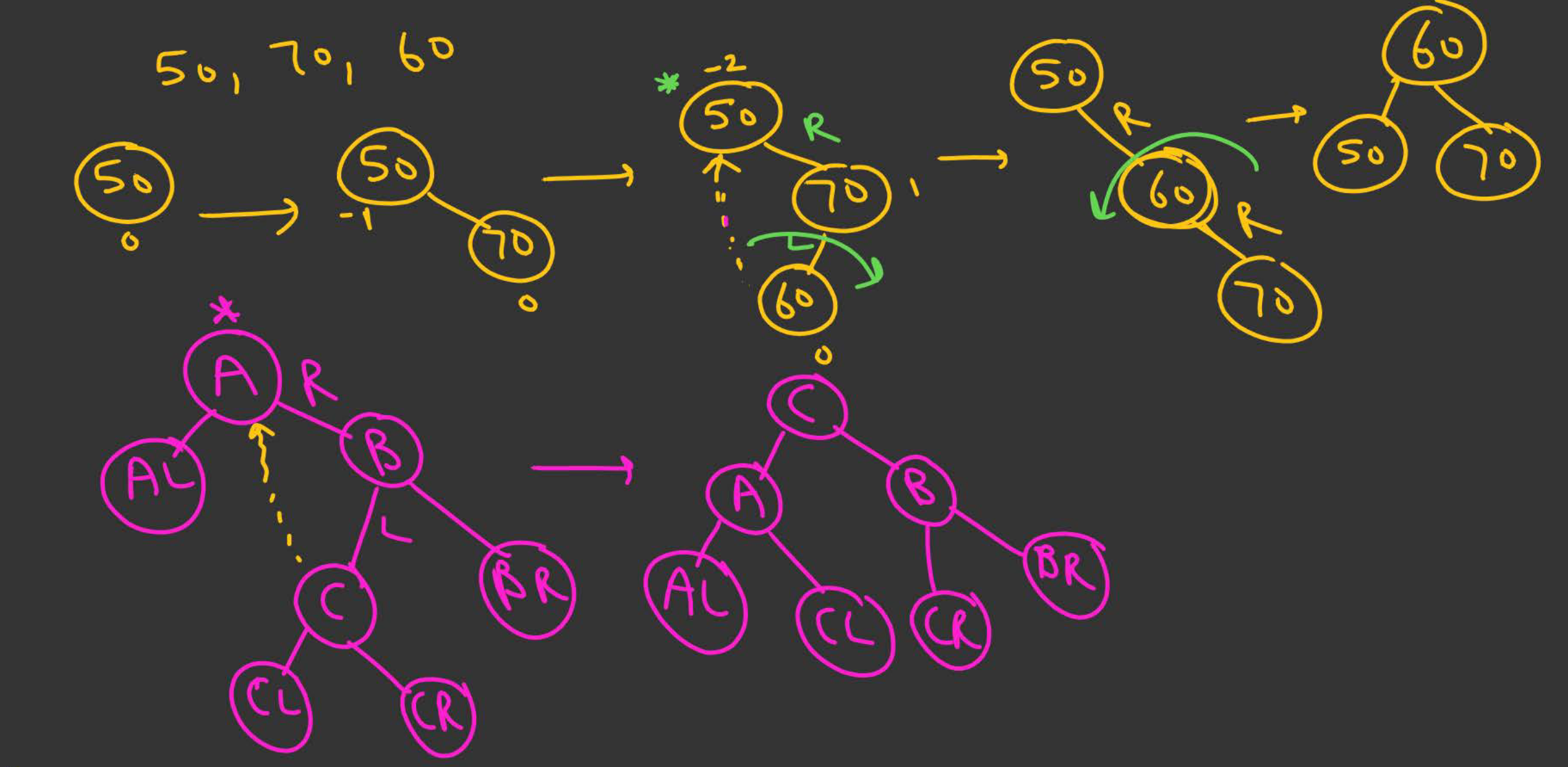
LR Rotation

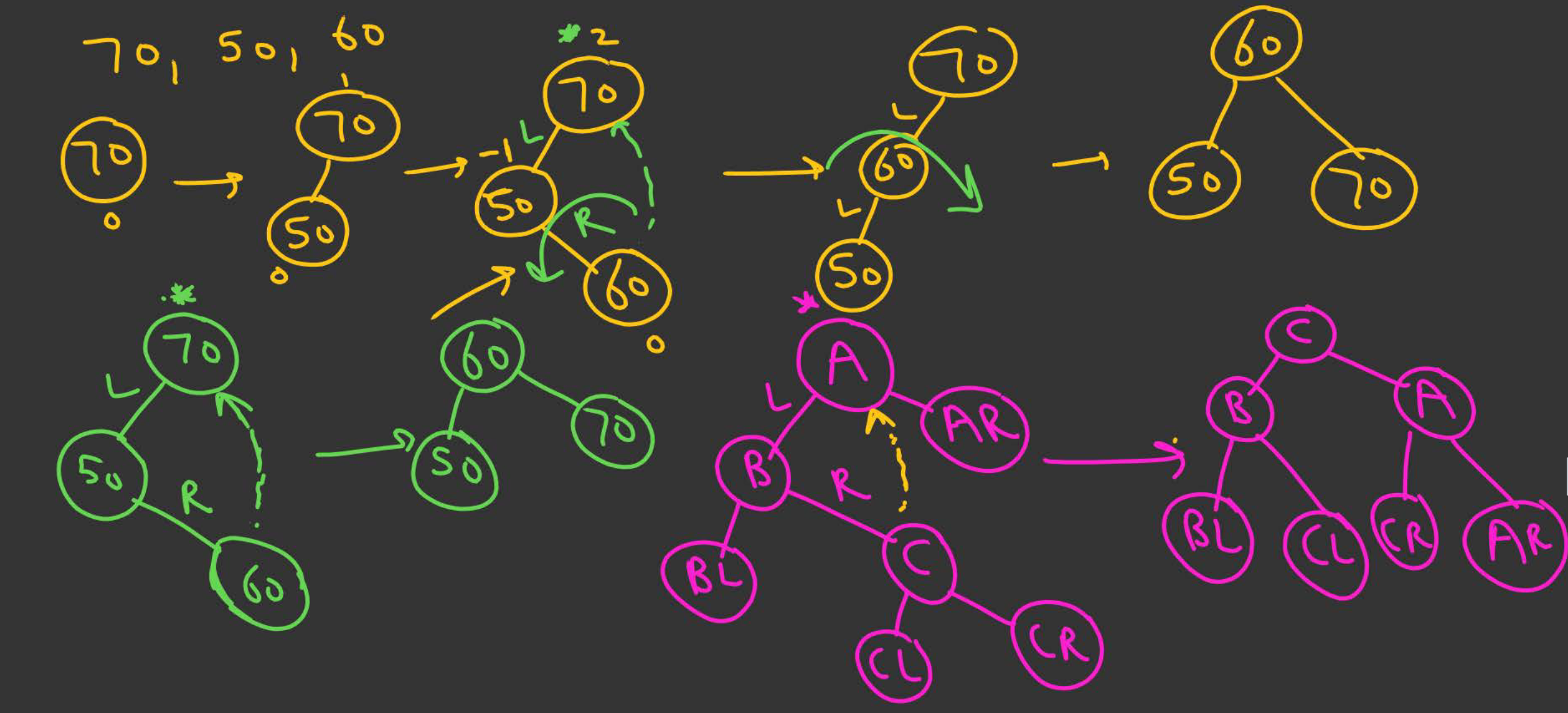
Done when insertion of a new node happens in the right subtree of the left child of a critical node.

• Let A be the first critical node from the bottom.
• Let B be A’s left child.
• Let C be B’s right child
• Perform a single left rotation on B:
  • C becomes parent of B.
  • B becomes the left child of C.
  • C’s left subtree becomes B’s right subtree.
• Perform a single right rotation on A:
  • C becomes the new root of this subtree.
  • A becomes the right child of C.
  • C’s right subtree becomes A’s left subtree.

RL Rotation

Done when insertion of a new node happens in the left subtree of the right child of a critical node.

• Let A be the first critical node from the bottom.
• Let B be A’s right child.
• Let C be B’s left child.
• Perform a single right rotation on B:
  • C becomes parent of B.
  • B becomes the right child of C.
  • C’s right subtree becomes B’s left subtree.
• Perform a single left rotation on A:
  • C becomes the new root of this subtree.
  • A becomes the left child of C.
  • C’s left subtree becomes A’s right subtree.