Sorting Algorithms

Table of Contents

• Summary
• Sorting Algorithms
  • Types of Sorting Algorithms
  • Other classifications
    • In-place Sorting Algorithm
    • Stable Sorting Algorithm
    • Inversion in an Array
• Bubble Sort
  • Algo1
  • Algo2
  • Algo3 (default)
  • Properties
• Selection Sort
  • Pseudocode and TC
  • Properties
• Insertion Sort
  • Pseudocode and TC
  • Properties
• Radix Sort
  • Properties
• Questions

Definition - Arrangement/Ordering of items in a sequence based upon some condition is Sorting.

Summary

Algorithm	Best Case TC	Worst Case TC	Special TC	In-place	Stable	SC
Bubble Sort	$\Omega (n)$	$O(n^2)$	-	✅	✅	$O(1)$
Selection Sort	$\Omega (n^2)$	$O(n^2)$	Better worst case no. of swaps than Bubble Sort	✅	❌	$O(1)$
Insertion Sort	$\Omega (n)$	$O(n^2)$	$O(n+d)$ if pre-sorted	✅	✅	$O(1)$
Radix Sort	-	-	$\Theta (n\ast d)$ input-independent	❌	✅	$O(n)$
Merge Sort	-	-	$\Theta (nlo{g}_{2}n)$ input-independent	❌	✅	$O(n)$ Aux mem + Recur. stack
Quick Sort	$\Omega (nlo{g}_{2}n)$	$O(n^2)$	Worst case for sorted	❌	❌	$O(n)$

Sorting Algorithms

1. Bubble Sort
2. Selection Sort
3. Insertion Sort
4. Merge Sort
5. Quick Sort
6. Heap Sort
7. Radix Sort

Types of Sorting Algorithms

1. Comparison Based - When an element is compared with other elements of the given data to achieve sorting.
2. Non-Comparison Based - When sorting is achieved without any comparison between the elements.

Other classifications

1. Iterative vs Recursive
2. Inplace vs Not-inplace
3. Internal (Only Main memory usage) vs External (Main + Secondary memory)
4. Stable vs Unstable

In-place Sorting Algorithm

Auxiliary memory is the memory space required by a program. Auxiliary memory requirement -

1. At most $O(1)$ (excluding recursion stack)
2. Recursion stack at most $O(logn)$

Stable Sorting Algorithm

If $A[i]=A[j]$ (not necessarily equal, just have the same priority of ordering) and in the given input $A[i]$ occurs before $A[j]$, then if in the sorting output too $A[i]$ occurs before $A[j]$ we say that the algorithm in stable.

Inversion in an Array

If $A[i]>A[j]$ but $i<j$, then $(i,j)$ is an inversion pair.

The time complexity of any Comparison based Sorting Algorithm depends upon two things-

1. The number of comparisons.
2. The number of inversions (Number of swaps).

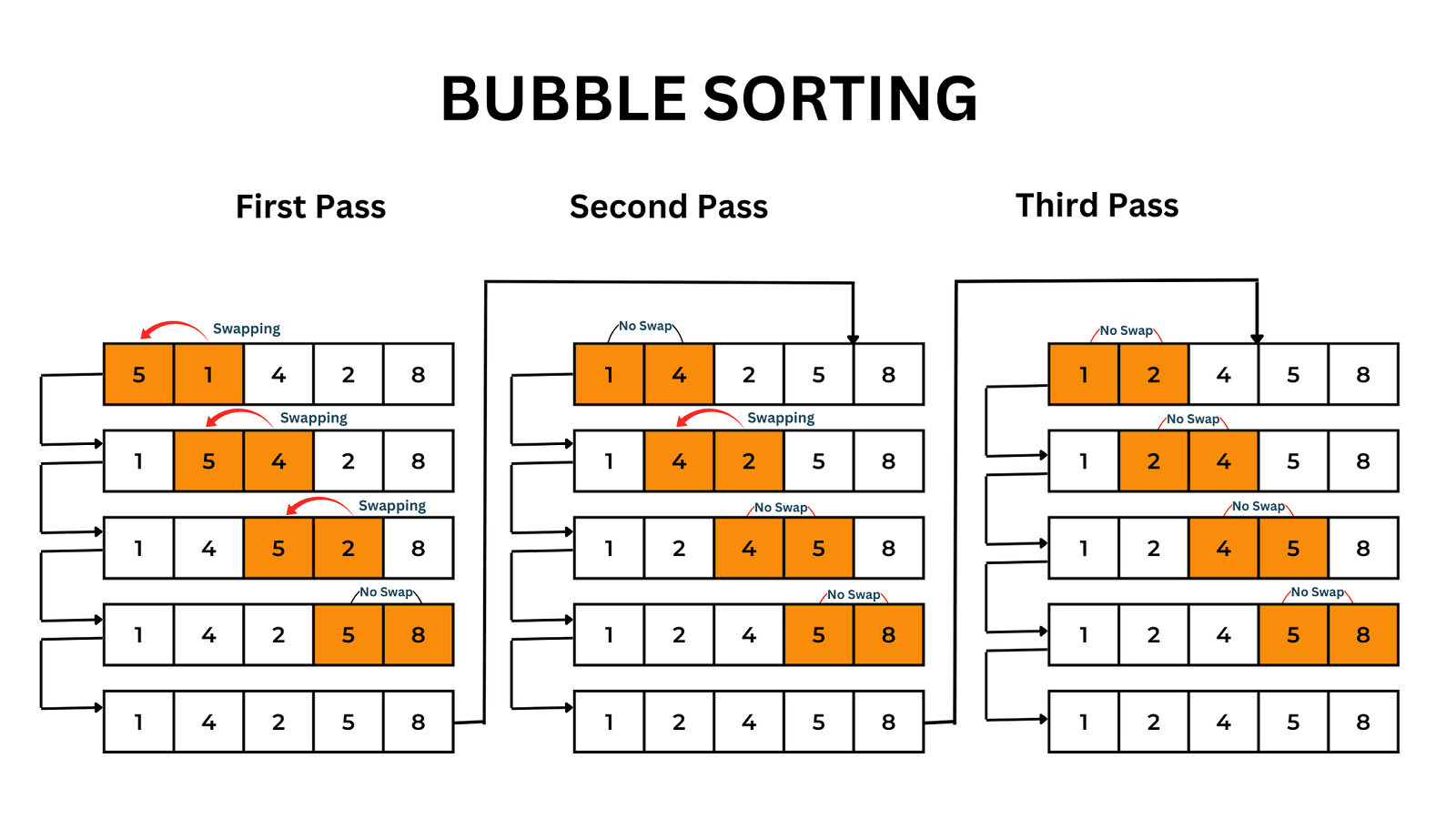
Bubble Sort

Bubble sort works in “passes”. If checks for each index whether the current element and the element after are forming an inversion pair. If an inversion pair is formed then we swap the elements, else we skip.

Algo1

1. BubbleSort1(A,n) {
2.   for (pass=1; pass<=n-1; pass++) {
3. 		for (j=1; j<=n-1; j++) {
4. 			if (A[j] > A[j+1]) {
5. 				swap(A[j], A[j+1])
6. 			}
7. 		}
8. 	 }
9. }

	No. of Comparisons	No. of Swaps
Best Case (Ascending Order)	$(n-1{)}^2$	$0$
Worst Case (Descending Order)	$(n-1{)}^2$	$(n-1)+(n-2)+\cdots +1=\frac{n(n-1)}{2}$

Algo2

As any $k^{th}$ pass would already fix $k$ large elements at their correct positions, we don’t need to run each pass $n-1$ times.

1. BubbleSort1(A,n) {
2.   for (pass=1; pass<=n-1; pass++) {
3. 		for (j=1; j<=n-pass; j++) {
4. 			if (A[j] > A[j+1]) {
5. 				swap(A[j], A[j+1])
6. 			}
7. 		}
8. 	 }
9. }

	No. of Comparisons	No. of Swaps	Complexity
Best Case (Ascending Order)	$\frac{n(n-1)}{2}$	$0$	$\Omega (n^2)$
Worst Case (Descending Order)	$\frac{n(n-1)}{2}$	$\frac{n(n-1)}{2}$	$O(n^2)$
Overall			$\Theta (n^2)$

Algo3 (default)

When number of swaps in the current arrangement is $0$, we can say that the array has been sorted and avoid unnecessary further passes.

BubbleSort1(A,n) {
	for (pass=1; pass<=n-1; pass++) {
		flag=0
  		for (j=1; j<=n-pass; j++) {
 			if (A[j] > A[j+1]) {
 				swap(A[j], A[j+1])
				flag=1
 			}
 		}
   
	   if (flag==1) {break}
	}
}

	No. of Comparisons	No. of Swaps	Complexity
Best Case (Ascending Order)	$n-1$	$0$	$\Omega (n)$
Worst Case (Descending Order)	$\frac{n(n-1)}{2}$	$\frac{n(n-1)}{2}$	$O(n^2)$

Properties

1. Is In-place, $SC=O(1)$.
2. Is Stable.
3. No. of swaps = No. of inversions.
4. Requires no swaps in best case scenario and $O(n^2)$ swaps in worst case scenario.
5. Guarantee - After some $k^{th}$ pass the $k$ largest elements are at their correct positions at the end of the array.
6. The maximum number of passes required - $(n-1)$.

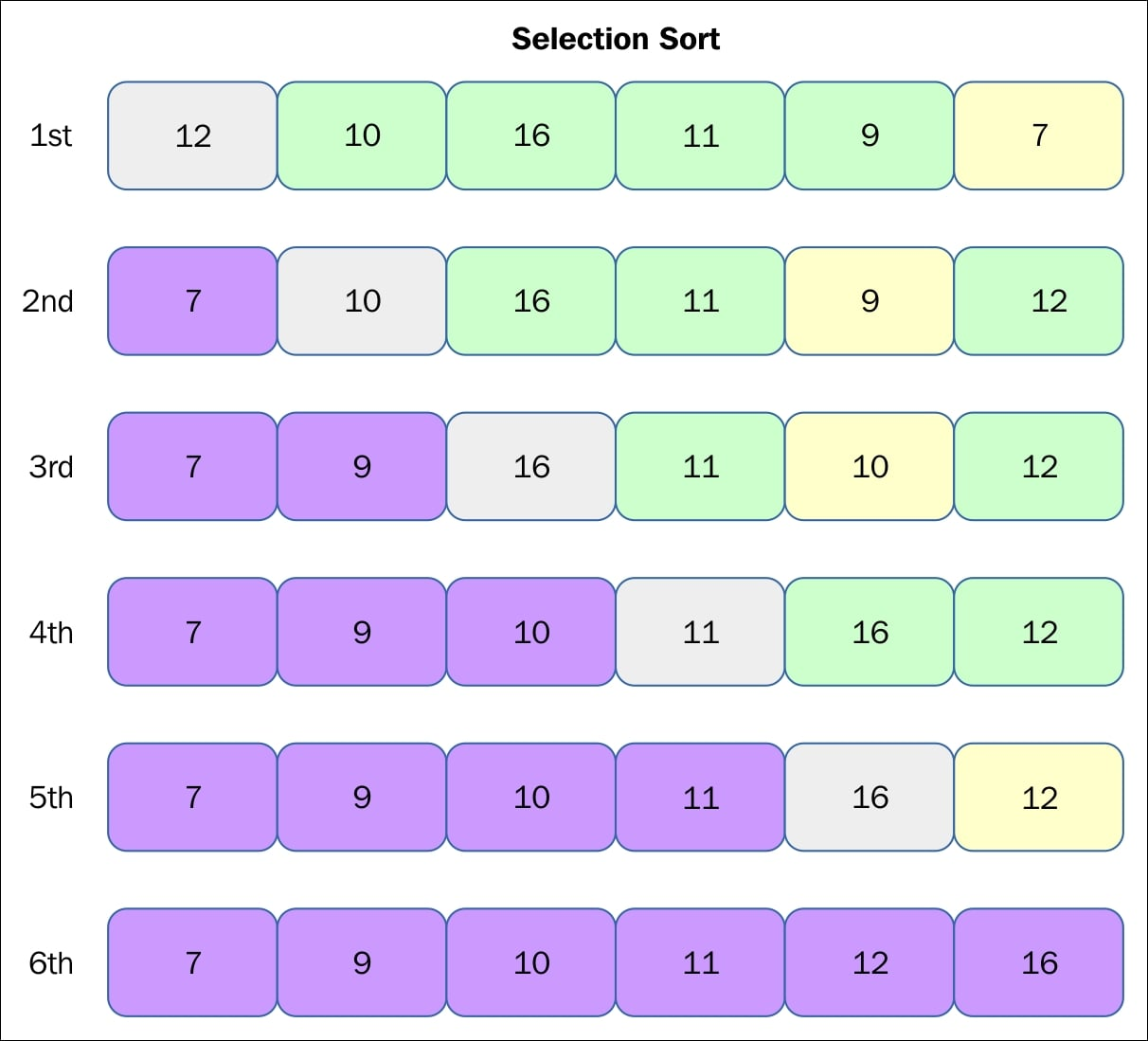
Selection Sort

1. In the $i^{th}$ pass, find the index with the $i^{th}$ smallest element.
2. Swap the element at the $i^{th}$ index with the $i^{th}$ smallest element.
3. Repeat until array is sorted

Pseudocode and TC

SelectionSort(A, n) {
	for (pass=1; pass<=n-1; pass++) {
		min=pass
		for (j=pass+1; j<=n; j++) {
			if A[j] < A[min] {
				min=j
			}
		}
		
		if min != pass {
            swap(A[pass], A[min])
        }
	}
}

	No. of Comparisons	No. of Swaps	Complexity
Best Case (Ascending Order)	$\frac{n(n-1)}{2}$	$0$	$\Omega (n^2)$
Worst Case (Descending Order)	$\frac{n(n-1)}{2}$	$n-1$	$O(n^2)$
Overall			$\Theta (n^2)$
Even though the overall best case time complexity is worse than Bubble sort, even under worst case the algorithm only takes $O(n)$ time complexity for the swaps.

Properties

1. Is Unstable.
2. Is In-place, $SC=O(1)$..
3. Always takes $n-1$ passes.
4. Each pass does exactly $1$ swap.

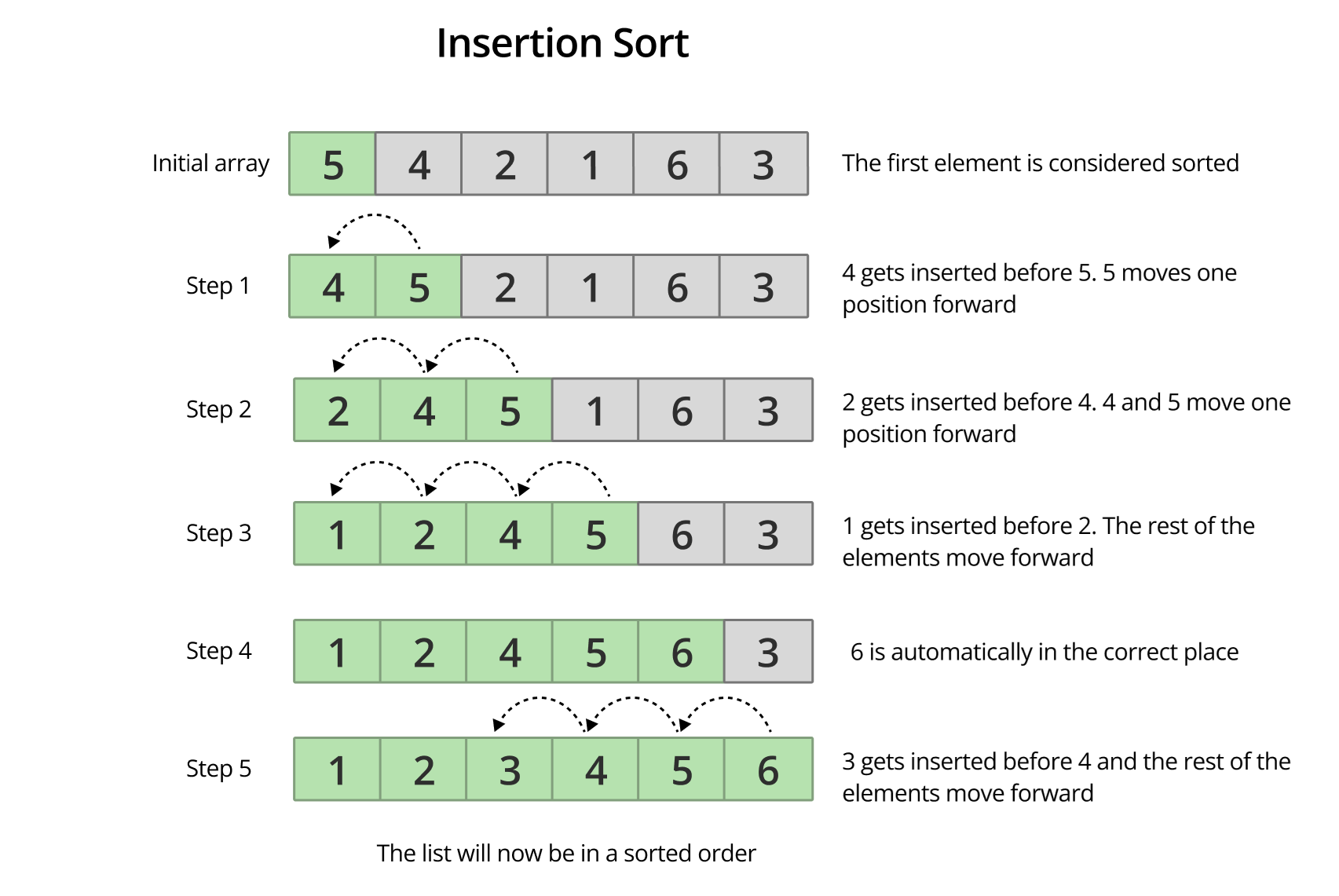
Insertion Sort

1. Pick elements from left to right one by one as key elements.
2. If the key element is less than the element at the key-1 index, swap them.
3. Keep swapping until there are no more elements to the left of key or the element at key-1 is greater than key element.

Pseudocode and TC

InsertionSort(A, n) {
	for (i=2; i<=n; i++) {
		key=A[i]
		j=i-1
		
		while (j > 0 and A[j]>key) {
			A[j+1]=A[j]
			j--
		}
		
		if (i != j+1) {
			A[j+1]=key
		}
	}
}

	No. of Comparisons	No. of Swaps	Complexity
Best Case (Ascending Order)	$n-1$	$0$	$\Omega (n)$
Worst Case (Descending Order)	$\frac{n(n-1)}{2}$	$\frac{n(n-1)}{2}$	$O(n^2)$

Properties

1. Is In-place, $SC=O(1)$.
2. Is Stable.
3. Always takes $n-1$ passes.
4. No. of swaps = No. of inversions.
5. If the input list is already pre-sorted, then it takes time of $O(n+d)$ where - $n$ = no. of elements $d$ = no. of inversions Check Question 2 for this.

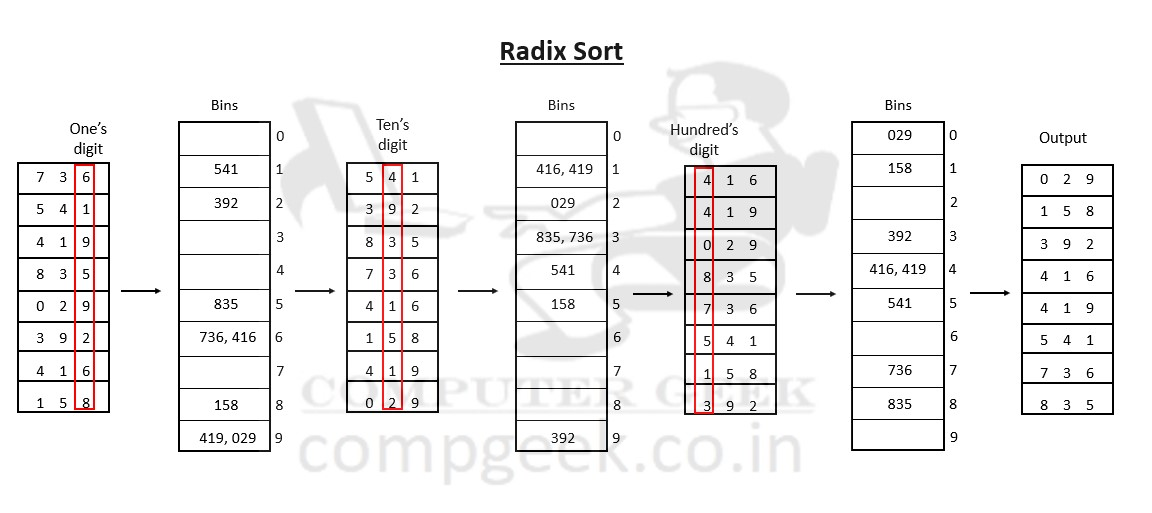
Radix Sort

Radix means the base of the number system.

1. Bin the numbers based on their unit’s digit using a key-value structure with keys 0–9, inserting elements for each key in FIFO order.
2. Collect the numbers by reading the bins from key 0 to 9, preserving order.
3. Repeat the above steps for the tens digit, then the hundreds digit, and so on.
4. Continue for k passes, where k is the number of digits in the maximum element.
5. The final array obtained is sorted.

Properties

1. Not In-place, requires external data structure with $SC=O(n)$.
2. Is Stable.
3. $TC=O(d\ast (n+b))\approx O(n\ast d)$. $b=$ base of given input. $d=$ no. of digits in the maximum element of the array. $n=$ no. of elements in the array.

Questions

Q1)

Sol${}^n$ - The time complexity of Radix Sort is $O(n\ast d)$ where $d$ is the number of digits in the maximum element of the array.

The maximum element of the array is $n^k$ and the number of digits in it are $lo{g}_{10}{n}^k+1=O(k\ast lo{g}_{10}n)$. So $TC=O(n\ast k\ast lo{g}_{10}n)=O(n\ast k\ast lo{g}_{10}n)$ as $k$ is some constant which wouldn’t affect the time complexity of the algorithm.

---

Q2)

Sol${}^n$ - The time complexity of Insertion sort for pre-sorted inputs is $O(n+d)$ where $d$ is the number of inversions. Here the permutations can have at most $n$ inversions so the time complexity is $O(n+n)=O(n)$.