Greedy Algorithms

Table of Contents

• Types of Problems
• Knapsack Problem
  • Problem Statement
  • Objective
  • Types of Knapsack
  • How to solve
• Job Scheduling with Deadline (JSD)
  • Problem Statement
  • Objective
  • How to solve
• Optimal Merge Patterns
  • Problem Statement
  • Objective
  • How to solve
• Encoding & Huffman Encoding
  • Huffman Encoding
• Minimum Cost Spanning Tree
  • Spanning Tree
  • Prim’s Vs Kruskal’s Algorithm
  • Djikstra’s MCST Algorithm
• Questions

Definition - Greedy algorithms focus on finding the local optima. They pick the option that best satisfy the criteria of problem. Example - Best First Search.

Types of Problems

1. Optimization Problems

   1. Requires a deterministic min/max value for a given criteria.
   2. Requires an objective function.
   3. Has optimal solutions.
   4. Example – Knapsack, Shortest Path.

2. Planning / Decision Problems

   1. Result is always either True / False.
   2. Doesn’t need an objective function.
   3. Doesn’t have optimal solutions, has feasible solutions.
   4. Example – Searching, Sorting, N-Queens.

Knapsack Problem

Problem Statement

You are given a set of $n$ objects, where each object iii has:

• a weight $w_i$​,
• a profit (or value) $p_i$​.
• a knapsack with a maximum capacity of $m$ units of weight

Objective

Select a subset of the objects such that:

• the total weight of the selected objects does not exceed the knapsack capacity mmm,
• each object is either included or excluded (for 1 knapsack) or partially selected (for fractional knapsack),
• the total profit of the selected objects is maximized.

Objective:

$$\max \sum x_i{p}_i\text{subject to}\sum x_i{w}_i\le m\text{where}{x}_i\in \{0,1\}\text{or}[0,1]$$

Types of Knapsack -

1. Fractional Knapsack - Partial objects are allowed, $0\le x_i\le 1$ Solved using Greedy methods.
2. Binary Knapsack (0/1 Knapsack) - No partial objects are allowed, $x_1\in \{0,1\}$ Solved using Dynamic Programming.

How to solve -

1. A greedy algorithm can always provide an optimal solution for a Fractional Knapsack problem.
   • Calculate the profit/weight ratio.
   • Assign priority to objects in descending order of ratio.
   • If the weight constraint satisfies, pick a whole/fraction of the object.
   • When the weight constraint fails, stop picking.
2. A greedy algorithm can’t always provide an optimal solution for a 0/1 Knapsack problem.

Job Scheduling with Deadline (JSD)

Problem Statement

You are given a set of $n$ jobs, where each job has:

• a arrival time $AT=0$ (each job is available from the start)
• a burst time $BT=1$ (unit execution time (each job takes exactly 1 unit of time))
• a deadline $d_i$​ (latest time by which it must be completed),
• a profit $p_i$​ earned if the job is completed on or before its deadline,

Objective

Schedule a subset of $m$ jobs such that:

• no two jobs overlap (only one job can be done at a time),
• each job finishes on or before its deadline,
• the total profit is maximized.

How to solve -

Suppose we have -

Jobs	Deadline $(D_i)$	Profit $(P_i)$
J1	2	200
J2	1	30
J3	2	50
J4	1	80

Brute Force -

Choose all subsets of the above $n$ jobs and calculate the total profit. The subset which provides the maximum profit is the answer. $TC=O(2^n)$

Greedy Algorithm -

1. Assign priority to jobs based upon the descending order of Profit.
2. Identify the max deadline $max(D)$ and store it.
3. Pick jobs in order of this priority and place each at its respective deadline $D_i$. If the deadline is not available, then try to place it at $D_i-1$.

$$\begin{array}{c}\begin{array}{cc}{J}_4& J_1\\ D_1& D_2\end{array}\end{array}$$

1. In the above schedule the priority will be J1, J4, J3, J2.
2. Pick J1. As $D_1=2$, check 2. As 2 is empty, J1 is assigned to 2.
3. Pick J4. As $D_4=1$, check 1. As 1 is empty, J4 is assigned to 1. Thus total profit is $200+80=280$.

Optimal Merge Patterns

This is an application of the merging algorithm.

Problem Statement

• You are given $n$ files.
• It is required to merge them using 2-way merging.

Objective

In which sequence should the files be merged such that:

• Total number of record movements is minimal.

How to solve -

Given $2$ sorted files $A$ and $B$ having $n$ and $m$ records respectively. To merge them into a single sorted file, we’d require $(m+n)$ record movements.

This is different from the merging in merge sort as it has element comparisons, while here we have record movements.

Example -

Suppose $A$, $B$, and $C$ have $10$, $15$, and $5$ records respectively. If we were to merge these files in the order $A\to B\to C$, what would be the total number of record movements?

Here we first merge $A$ and $B$ into one file, and then merge this resultant file with $C$. So -

1. Record movements in merging $A$ and $B$ - $10+15=25$. $[I]$
2. Resultant file $AB$ now has $25$ records.
3. Record movements in merging $AB$ and $C$ - $25+5=30$. $[II]$
4. Resultant file $ABC$ now has $30$ records.
5. Using $I$ and $II$, total number of record movements $=\boxed{25+30=55}$.

However, if we were to merge in the sequence $B\to C\to A$, the total number of record movements will be $50$.

Brute Force

Try all permutations of the $n$ files and calculate the total number of record movements. The permutation which provides the minimum record movements is the answer. $TC=O(n!)$

Greedy Algorithm

1. Assign priority to files in an ascending order of record count.
2. Pick two files with the highest priorities. Merge them and add the resulting file again into the list and recalculate priorities.
3. Keep merging until all files are merged and only one file remains in the queue.

In the above example, the priority would be $C,A,B$ thus $C\to A\to B$ would provide the minimum record movements of $\boxed{45}$.

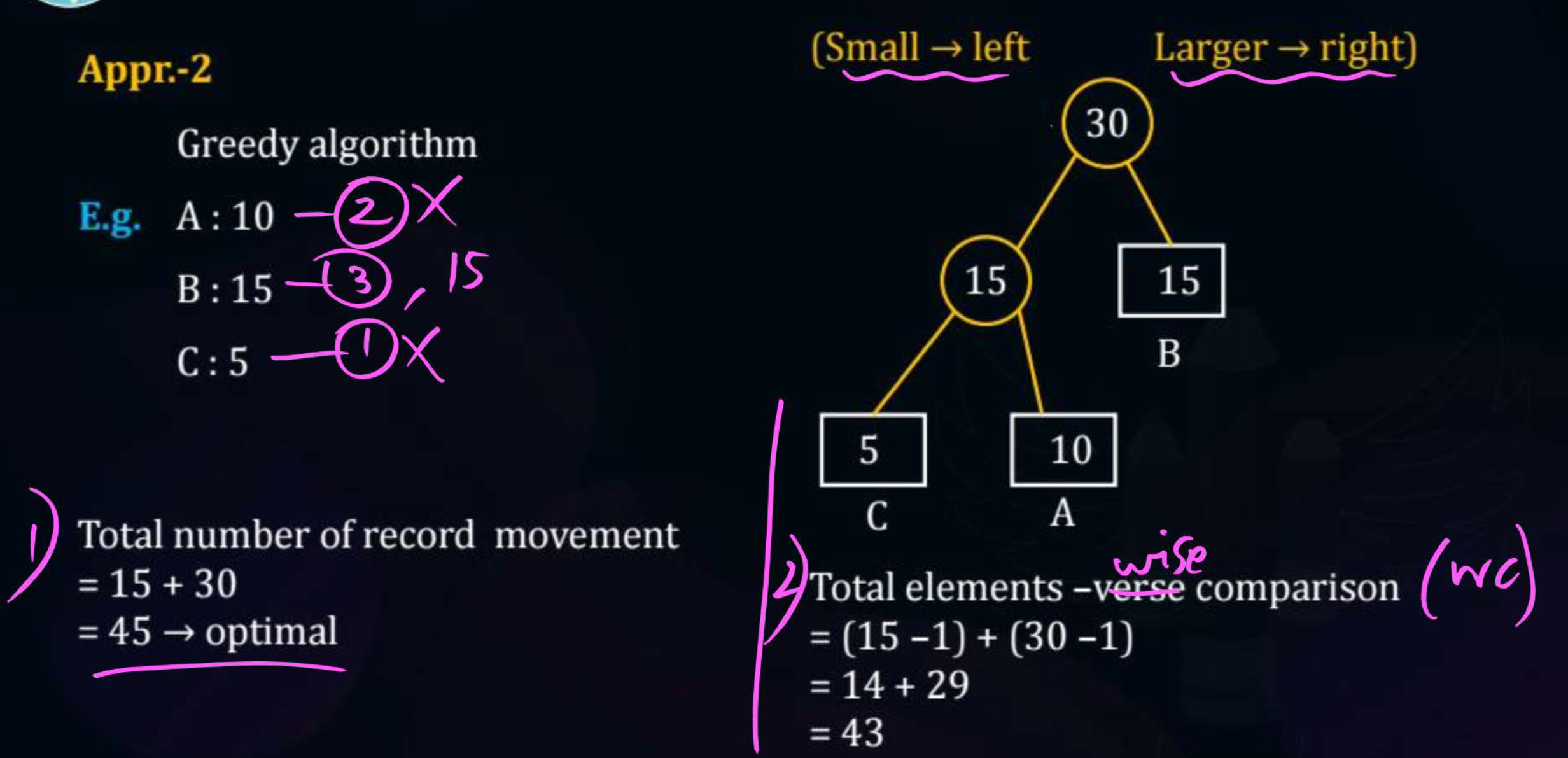
1. Total number of record movements - $m+n$
2. Total number of element-wise comparison - $m+n-1$

Merge Tree

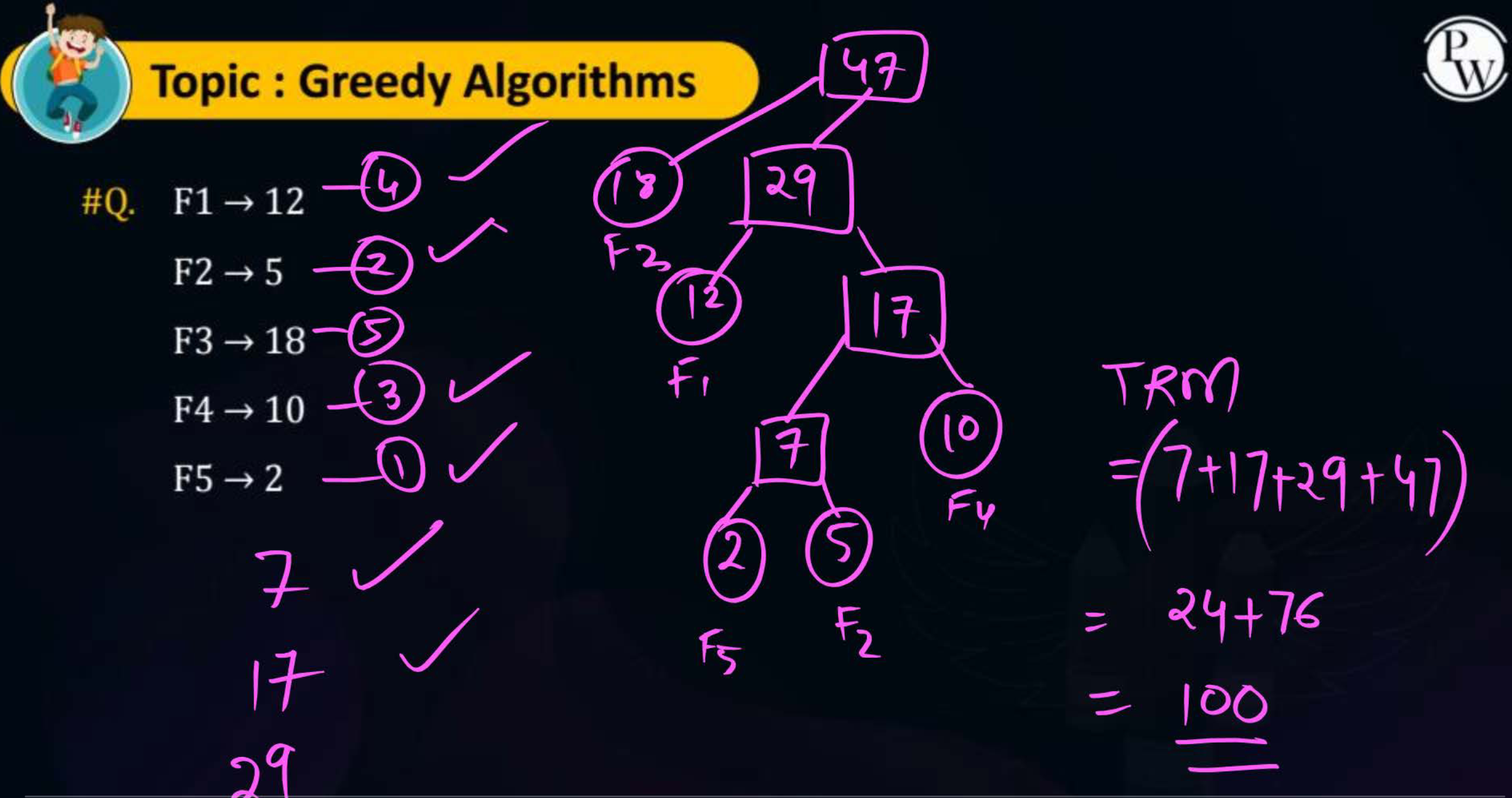
We can use a merge tree too where the files with smaller size are at the bottom of the tree while the files with larger size are closer to the root.

Formally we do ${\sum }_{i=1}^n{d}_i{q}_i$ where $d_i$ is the depth of a file in the merge tree (excluding the root node) and $q_i$ is the size of that file. From the tree above we can see -

• F1 is at depth 2, thus $d_1=2$

• Similarly, $d_2=4$

• $d_3=1$

• $d_4=3$

• $d_5=4$ Thus record movements $=2\ast 12+4\ast 5+1\ast 18+3\ast 10+4\ast 2=24+20+18+30+8=\boxed{100}$

• At any node of the tree, the smaller child is to the left and the larger child is to the right.

• Smaller files are kept at the bottom because the cost of repeatedly merging them would be smaller.

Encoding & Huffman Encoding

Definition - Encoding is the process of converting information from one format to another for efficient transmission or storage.

Types of Encoding -

1. Uniform Encoding - Each character is encoded using equal number of bits.
2. Non-uniform Encoding - The number of bits used to encode a character depend upon some criteria.

A problem with Uniform Encoding techniques like Binary Encoding is the wastage of space. For example - To encode 10 characters using binary encoding we’d require 4 bits. But using 4 bits we can encode a total of 16 characters, so the extra 6 binary sequences are being wasted.

Huffman Encoding

A non-uniform encoding technique where the encoding/code is based upon the frequency of that character or elements.

1. Assign more bits to elements with a low frequency.
2. Assign less bits to elements with a high frequency.
3. No two elements have the same encoding, encoding is unique.

Suppose we have 5 characters with the following frequencies -

$$A-0.23,B-0.05,C-0.48,D-0.15,E-0.09$$

The 2-way Optimal Binary merge tree would look like -

Here the smaller child of every node is the left child node and the larger child of every node is the right child node. Let -

• Left Branch - 0
• Right Branch - 1

So the encodings for the characters are like -

$$A-10,B-1100,C-0,D-111,E-1101$$

To get the average number of bits/character, sum the intermediate nodes of the merge tree similar to how we sum to get the number of record movements. Here the average number of bits/character is $1.95$.

Minimum Cost Spanning Tree

Types of graphs -

1. In a directed complete graph there are $n-1$ edges for all $n$ vertices. Thus the total number of edges is - $n(n-1)=O(n^2)$.
2. In an undirected complete graph the first vertex has $n-1$ edges, second vertex has $n-2$ vertex, and so on. Thus the total number of edges is $\frac{n(n-1)}{2}=O(n^2)$.

Types of graph representations -

1. Adjacency Matrix - $O(n^2)$.
2. Adjacency List - $O(n+e)$.

When to use which representation -

1. For dense graphs we prefer Adjacency Matrix instead of Adjacency List as $e\approx O(n^2)$ for them. An Adjacency list would be of $O(n^2+n)$ while an Adjacency Matrix would be of $O(n^2)$.
2. For sparse graphs we prefer Adjacency Lists because the number of edges in them is low.

Spanning Tree

A subgraph $T(V,E^{\prime })$ of a given graph $(V,E)$ where $E^{\prime }\subset E$ is a spanning tree if $T$ is a tree (acyclic).

• A spanning tree with $n$ vertices will always have $\boxed{n-1}$ edges.
• Number of edges not used in the spanning tree - $e-(n-1)=\boxed{e-n+1}$
• Number of null links in the spanning tree - There are $2n$ links in the tree out of which $n-1$ are used. Thus $2n-(n-1)=2n-n+1=\boxed{n+1}$.

Prim’s Vs Kruskal’s Algorithm

• Prim’s - Pick the minimum cost edges extending from the nodes currently in the tree.
• Kruskal’s - Using a Min Heap + Set, greedily pick $n-1$ smallest cost edges.

1. Prim’s Algorithm
   • Time Complexity:
     • $O(n^2)$ (without heap)
     • $O(n+e)$ (with heap)
     • If $e\approx n^2$, then $O(n^2\log n)$
   • Always maintains a tree structure
2. Kruskal’s Algorithm
   • Time Complexity: $O(e\log e)$ (uses heap)
   • May or may not maintain a tree structure during execution
3. The cost of the MCST obtained by both algorithms is the same.
4. The tree structure obtained by both approaches:
   • If all edges have unique/distinct weights, both algorithms produce the same tree
   • If there are duplicate edge weights, the tree structure may or may not be the same

Djikstra’s MCST Algorithm

1. Consider all edges of the graph.
2. If a cycle forms, remove the maximum cost edge in that cycle.

Djikstra’s Single Source Shortest Path is also a Greedy Algorithm, but discussed under Dynamic Programming.

---

Questions

Q1) We have 6 files of the following sizes, how can we merge them to get the minimum number of record movements?

$$A-5,B-12,C-10,D-11,E-20,F-25$$

Sol${}^n$ - Here the priority would be - $A,C,D,B,E,F$. The merge tree would look something like this - 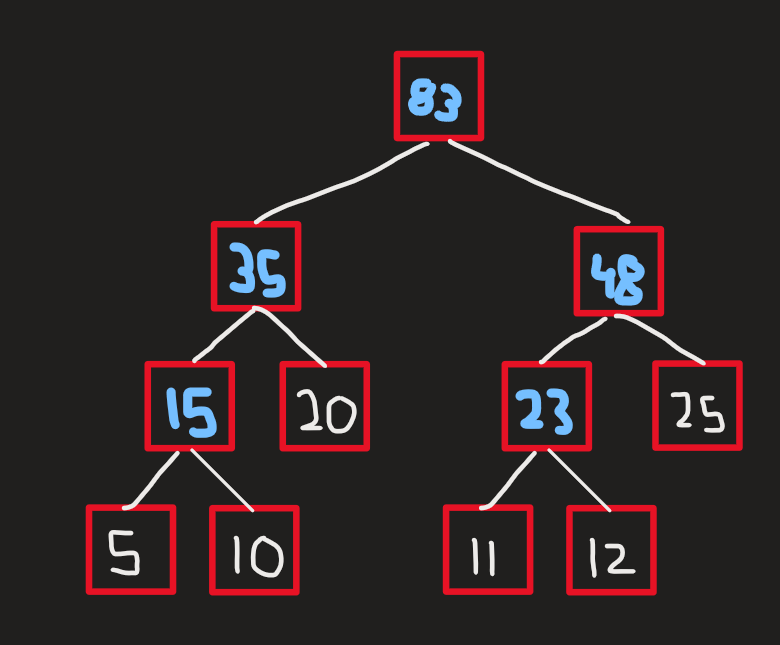Here the priority queue looked like -

• $5,10,11,12,20,25$. Pick $5$ and $10$ and merge. Resultant = $15$.
• $11,12,15,20,25$. Pick $11$ and $12$ and merge. Resultant = $23$.
• $15,20,23,25$. Pick $15$ and $20$ and merge. Resultant = $35$.
• $23,25,35$. Pick $23$ and $25$ and merge. Resultant = $48$.
• $35,48$. Pick $35$ and $48$ and merge. Resultant = $83$.
• $83$. Only one file remains, thus merging terminates.

Total record movement = $15+23+35+48+83=\boxed{204}$

---

Q2) What is the worst case no. of element wise comparison in the previous question?

Sol${}^n$ - The worst case number of comparisons are $m+n-1$. So in each file merge the worst case number of comparisons is -

• Upon merging $5,10\to 5+10-1=14$
• Upon merging $11,12\to 11+12-1=22$
• Upon merging $15,20\to 34$
• Upon merging $23,25\to 47$
• Upon merging $35,48\to 82$

Total = $14+22+34+47+82=\boxed{199}$

$$\text{(OR)}$$

Just do $\text{No. of record movements - No. of merges}=204-5=\boxed{199}$.

---

Q3) What is the bet case no. of element wise comparison in the previous question?

Sol${}^n$ - The best case number of comparisons are $min(m,n)$. So in each file merge the best case number of comparisons is -

• Upon merging $5,10\to min(5,10)=5$
• Upon merging $11,12\to min(11,12)=11$
• Upon merging $15,20\to 15$
• Upon merging $23,25\to 23$
• Upon merging $35,48\to 35$

Total = $5+11+15+23+35=\boxed{89}$

---

Q4)

Sol${}^n$ - The merge tree for this is -

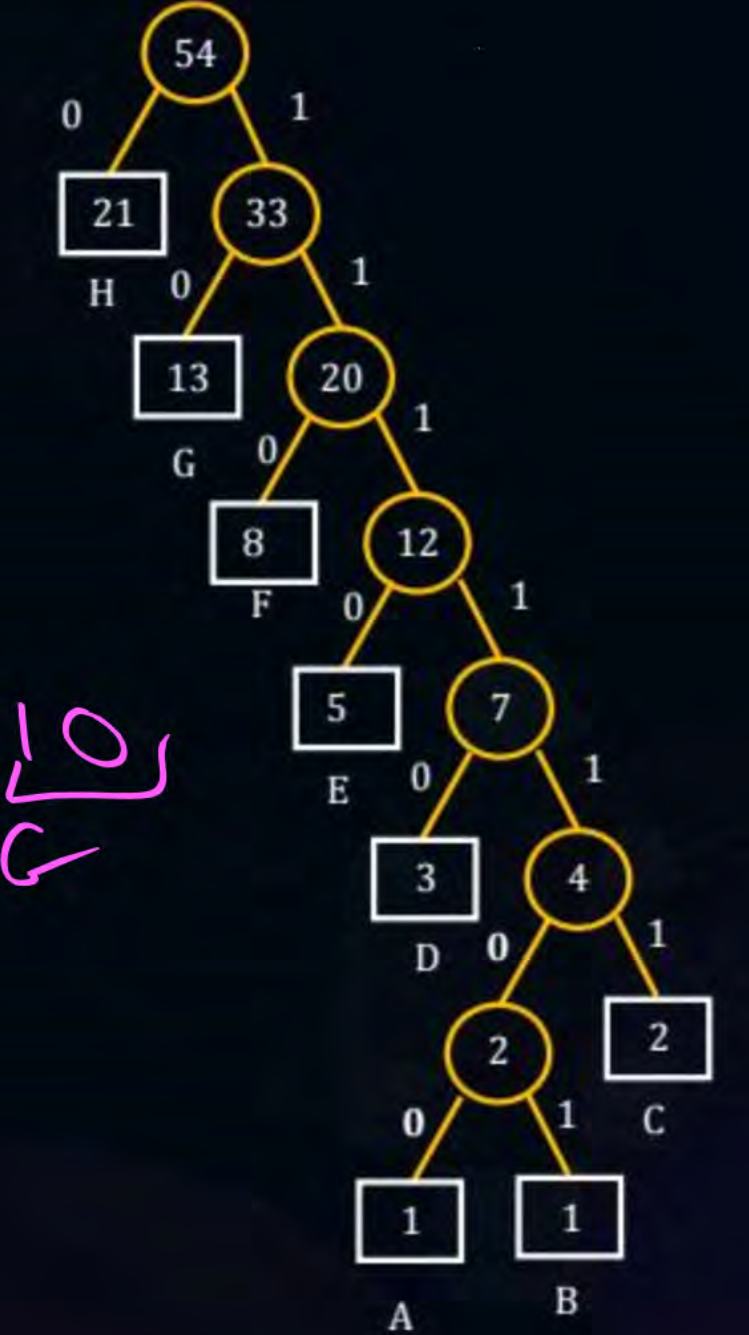
Due to this the encodings turn out to be like -

• H - 0
• G - 10
• F - 110
• E - 1110
• D - 11110
• C - 111110
• B - 111111
• A - 111110 So the encoding can be decoded like -

$$\underset{F}{\underbrace{110}}\underset{D}{\underbrace{11110}}\underset{H}{\underbrace{0}}\underset{E}{\underbrace{1110}}\underset{G}{\underbrace{10}}$$

Thus $\boxed{FDHEG}$ is the answer.

---

Q5)

Sol${}^n$ - Here the merge tree is like -

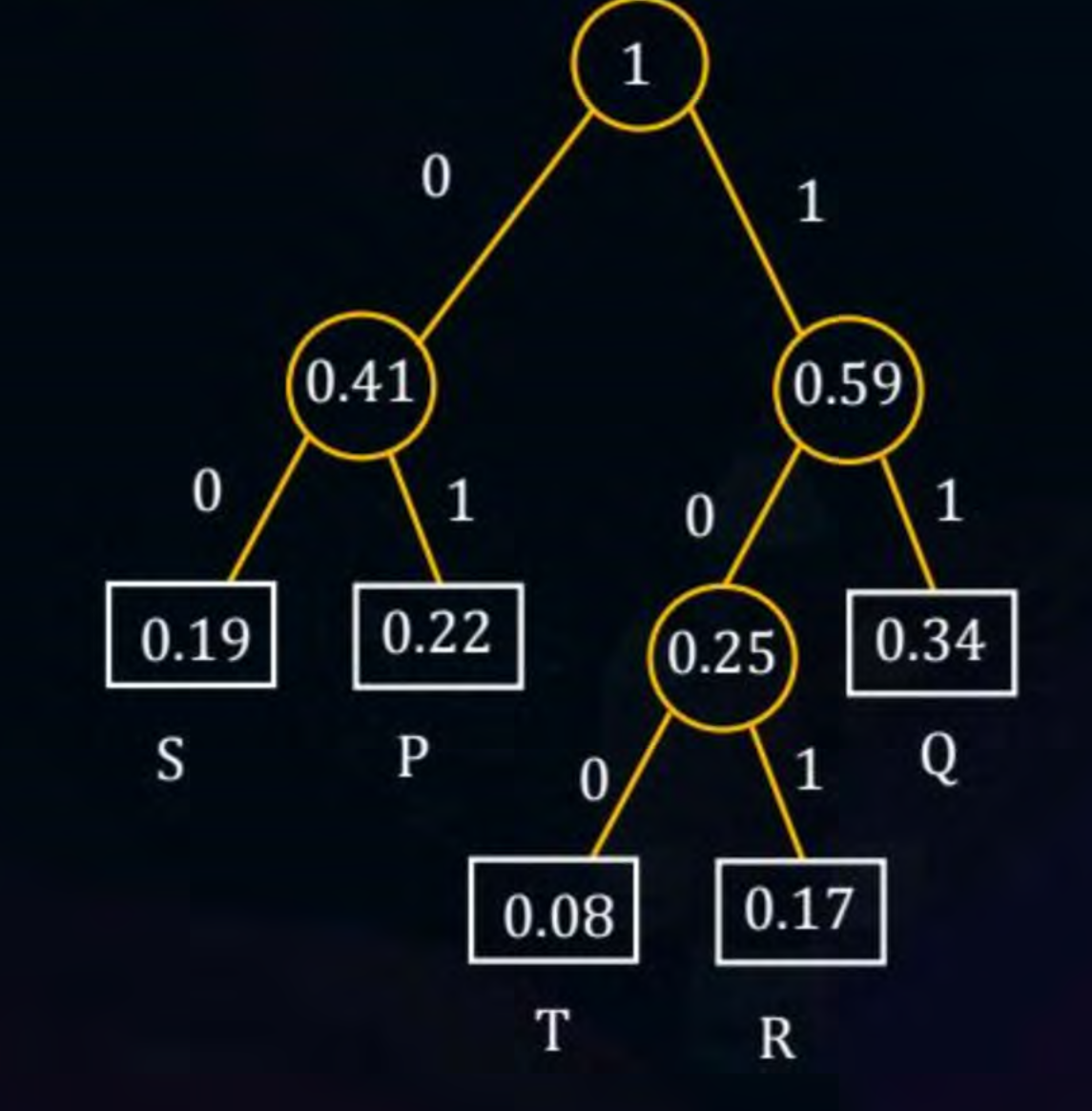
The average number of bits/characters $=1+0.41+0.59+0.25=2.25$. Thus for 100 characters, the expected length of the encoded message would be $2.25\ast 100=\boxed{225}$.

---

Q6)

Sol${}^n$ -

Here according to the second rule - $len(b)\le len(c)\le len(d)$. Thus $d$ should have a higher priority, then $c$ and lastly $b$. Using this information and frequency from the string we can make the merge tree -

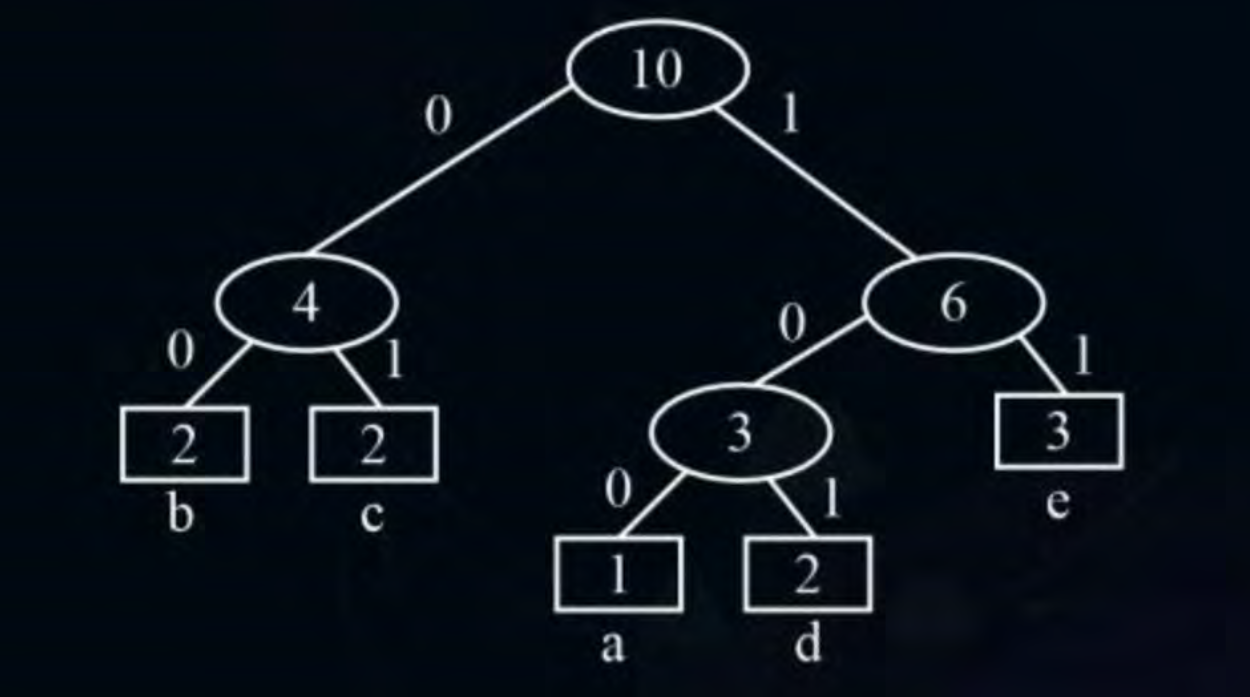
Using this we can find the encoding for each character and then find the total length of the encoded string. It would come out to be $\boxed{23}$.

---

Q7)

Sol${}^n$ - This can be solved using [[Greedy Algorithms#|Djikstra’s MCST Algorithm]]. Here there are 3 cycles. If some edge was not selected from a cycle for the MCST, then it had the maximum cost among all edges in that cycle.

• In cycle $A\to B\to C$, $AB$ was not selected. As $|BC|=2$ and $|AC|=9$, $|AB|>9$, thus $|AB|>10$.
• In cycle $E\to D\to F$, $|ED|>6$, thus $|ED|>7$.
• In cycle $B\to E\to D\to C$, $|CD|>15,thus$|CD|>16$.

Thus total cost = $36+10+7+16=\boxed{69}$.

---

Q8)

Sol${}^n$ - The minimum cost edges in such a graph would be between two adjacent nodes $V_i$ and $V_{i-1}$ of cost $2$. As there are a total $n-1$ edges, cost of the MCST would be $\boxed{2n-2}$.

---

Q9)

$\underline{{\text{Sol}}^n}-$

• The graph will be the XY coordinate plane with each $(x,y)$ coordinate being a vertex.
• Thus in total the graph will have $n^2$ vertices.
• The edges of such a graph will be of cost $1$ or $\sqrt{2}$.
• As the graph forms a grid (draw one if needed), one can simply follow the gridlines and traverse all vertices. Thus for such a path using edges of cost $1$ will be cheaper.
• The MCST would have $n^2-1$ edges ($n^2=$ No. of vertices) and as each edge will be of cost 1, the total cost would be $\boxed{n^2-1}$.